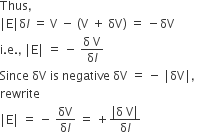CBSE
Class 10 Class 12
An equipotential surface is a surface with a constant value of the potential at all points on the surface. For a single charge q, the potential is given
by,
This shows that V is a constant if r is constant. Thus, equipotential surfaces of a single point charge are concentric spherical surfaces centre at the charge.
No work in done in moving from one point to another in the equipotential surface.

For a uniform electric field E, say, along with the x-axis, the equipotential surfaces are planes normal to the x-axis, i.e., planes parallel to the y-z plane.
(i) The electric field is in the direction in which the potential decreases steepest.
(ii) Its magnitude is given by the change in the magnitude of potential per unit displacement normal to the equipotential surface at the point.
Consider two closely spaced equipotential surfaces A and B Fig. with potential values V and V + δV, where δV is the change in V in the direction of the electric field E.
Let P be a point on the surface B. δl is the perpendicular distance of the surface A from P. Imagine that a unit positive charge is moved along this perpendicular from the surface B to surface A against the electric field. The work done in this process is |E|δl.
This work equals the potential difference VA –VB. Thus,