Short Answer TypeA 1.00 molar aqueous solution of trichloroacetic acid (CCl3COOH) is heated to its boiling point. The solution has the boiling point of 100.180C. Determine the van’t Hoff factor for trichloroacetic acid. (Kb for water = 0.512 kg mol-1)
Define the following terms:
(i) Mole fraction
(ii) Isotonic solutions
(iii) Van’t Hoff factor
(iv) Ideal solution
Calculate the amount of KCl which must be added to 1 kg of water so that the freezing point is depressed by 2K. (Kf for water = 1.86 K kg mol-1)
Long Answer Type(a) Differentiate between molarity and molality for a solution. How does a change in temperature influence their values?
(b) Calculate the freezing point of an aqueous solution containing 10.50 g of MgBr2in 200 g of water. (Molar mass of MgBr2 = 184 g) (Kf for water = 1.86 K kg mol-1)
(a) Define the terms osmosis and osmotic pressure. Is the osmotic pressure of a solution a colligative property? Explain.
(b) Calculate the boiling point of a solution prepared by adding 15.00 g of NaCl to 250.0 g of water. (Kb for water = 0.512 K kg mol-1), (Molar mass of NaCl = 58.44 g)
Short Answer TypeWhy does a solution containing non-volatile solute have higher boiling point than the pure solvent? Why is elevation of boiling point a colligative property?
Calculate the freezing point of the solution when 31 g of ethylene glycol (C2H6O2) is dissolved in 500 g of water. (Kf for water = 1.86 K kg mol–1)
Long Answer Type(a) State Raoult’s law for a solution containing volatile components.
How does Raoult’s law become a special case of Henry’s law?
(b) 1·00 g of a non-electrolyte solute dissolved in 50 g of benzene lowered the freezing point of benzene by 0·40 K. Find the molar mass of the solute. (Kf for benzene = 5·12 K kg mol-1)
(a) Let p1, p2 = Partial vapour pressure of two volatile components 1 and 2 of a mixture 
= Vapour pressure of pure components 1 and 2
x1, x2 = Mole fractions of the components 1 and 2
ptotal = Total vapour pressure of the mixture then Raoult’s law can be stated as: For a solution of volatile liquids, the partial vapour pressure of each component in the solution is directly proportional to its mole fraction.
That is, for component 1,
p1 
x1
And, p1 = 
x1
For component 2,
P2 = 
x2
According to Dalton’s law of partial pressures,
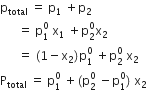
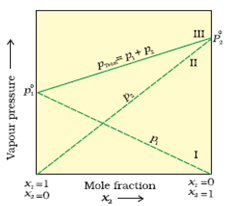
The plot of vapour pressure and mole fraction of an ideal solution at constant temperature is shown below.
Raoult’s Law as a Special Case of Henry’s Law
According to Raoult’s law, the vapour pressure of a volatile component in a given solution is p1 =
x1
According to Henry’s law, the partial vapour pressure of a gas (the component is so volatile that it exists as gas) in a liquid is
p = KH x
It can be observed that in both the equations, the partial vapour pressure of the volatile component varies directly with its mole fraction. Only the proportionality constants KH and are different. Thus, Raoult’s law becomes a special case of Henry’s law in which KH is equal to .
(b) Given: w2 = 1g (weight of solute)
w1 = 50 g (weight of solvent)
Tf = 0.40 K
kf = 5.12 K Kg mol-1
M2 =? (Molar mass of solute)
Using the equation,
Tf = Kfm (where m is molality)
0.40 = 5.12 x m
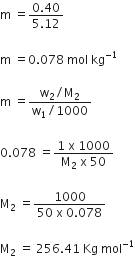
(a) Define the following terms:
(i) Ideal solution
(ii) Azeotrope
(iii) Osmotic pressure
(b) A solution of glucose (C6H12O6) in water is labeled as 10% by weight. What would be the molality of the solution?
(Molar mass of glucose = 180 g mol-1)
a) Define the following terms:
(i) Mole fraction
(ii) Ideal solution
(b) 15.0 g of an unknown molecular material is dissolved in 450 g of water. The resulting solution freezes at - 0.34°C. What is the molar mass of the material? (Kf for water = 1.86 K kg mol-1)
Switch
