253.

Prove that in an irreversible process:
∆S_(system) + ∆S_{(surroundings)} > 0

If any part of the process is irreversible, the process as a whole is irreversible. Suppose the total heat lost by the surrounding is q_irrev. This heat is absorbed by the system. However, entropy change of the system is always calculated from the heat absorbed reversibly.

 

This is because of the large size of the surroundings due to which heat lost (q_irrev) by the surroundings can be considered as the heat lost reversibly and isothermally at temperature T.
The total entropy change for the combined system and surroundings is



We know that the work done in a reversible process is the maximum work.

                        

Also, internal energy (U) is a state function, the value of U is same whether the process is carried out reversibly or irreversibly. Hence

     

From relation (4) and (5), we conclude that

                          


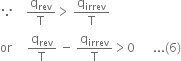
Combining the result with the result given in equation (3),
       

Thus, in an irreversible process, the entropy change for the combined system and the surroundings i.e. an isolated system is greater than zero i.e. an irreversible process is accompanied by a net increase of entropy.