Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Application of Derivatives

Name: Zigya - For The Curious Learner
Rating: 4.4 (740 reviews)

Short Answer Type

21. The surface area of a spherical bubble is increasing at the rate of 2 cm²/sec. Find the rate at which the volume of the bubble is increasing at the instant its radius is 6 cm.

223 Views

22.

The volume of a spherical balloon is increasing at the rate of 25 cm³/sec. Find the rate of change of its surface area at the instant when its radius is 5 cm.

87 Views

Long Answer Type

23. The radius of a spherical soap bubble is increasing at the rate of 0.3 cms^–1. Find the rate of change of its (i) volume (ii) surface area when the radius is 8 cm.

203 Views

24. The radius of a spherical soap bubble is increasing at the rate of 0.2 cms^–1. Find the rate of change of its (i) volume (ii) surface area, when the radius is 4 cm.

105 Views

25. The radius of a spherical soap bubble is increasing at the rate of 0.4 cms^–1 Find the rate of change of its (i) volume (ii) surface area, when the radius is 10 cm.

Let r be radius of spherical soap bubble.
$therefore space space space space space dr over dt space equals space 0.4 space space cm space straight s to the power of negative 1 end exponent space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space... left parenthesis 1 right parenthesis$
$left parenthesis straight i right parenthesis space space space space space space space space space space space space space straight V space equals space fraction numerator 4 straight pi over denominator 3 end fraction straight r cubed space space where space straight V space is space volume.$

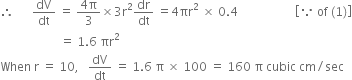
$therefore space space space space space space dV over dt space equals space fraction numerator 4 straight pi over denominator 3 end fraction cross times 3 straight r squared dr over dt space equals 4 πr squared space cross times space 0.4 space space space space space space space space space space space space space space space space space space space open square brackets because space of space left parenthesis 1 right parenthesis close square brackets space space space space space space space space space space space space space space space space space space space space equals space 1.6 space πr squared space When space straight r space equals space 10 comma space space space dV over dt space equals space 1.6 space straight pi space cross times space 100 space equals space 160 space straight pi space cubic space cm divided by sec$

(ii) Again, $straight S space equals space 4 πr squared comma space space space space where space straight S space is space surface space area.$

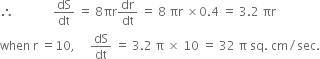
$therefore space space space space space space space space space space space space space dS over dt space equals space 8 πr dr over dt space equals space 8 space πr space cross times 0.4 space equals space 3.2 space πr space space space space space space space space space space space space space when space straight r space equals 10 comma space space space space space dS over dt space equals space 3.2 space straight pi space cross times space 10 space equals space 32 space straight pi space sq. space cm divided by sec.$

88 Views

Short Answer Type

26.

A ballon which always remains spherical on inflation, is being inflated by pumping in 900 cubic centimetres of gas per second. Find the rate of which the radius of the balloon is increasing when the radius is 15 cm.

93 Views

27.

The volume of a cube is increasing at a rate of 9 cubic centimeters per second. How fast is the surface area increasing when the length of an edge is 10 centimeters?

102 Views

28.

The volume of a cube is increasing at a rate of 7 cubic centimeters per second. How fast is the surface area increasing when the length of an edge is 12 centimeters?

74 Views

29. The volume of a cube is increasing at the rate of 8 cm³/s. How fast is the surface area increasing when the length of an edge is 12 cm?

105 Views

30.

The length x of a rectangle is decreasing at the rate of 2 cm/s and the width y is increasing at the rate of 2 cm/s. When x = 12 cm and y = 5 cm, find the rate of change of (a) the perimeter and (b) the area of the rectangle.

139 Views