Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Application of Derivatives

Name: Zigya - For The Curious Learner
Rating: 4.4 (740 reviews)

Short Answer Type

31.

The length x of a rectangle is decreasing at the rate of 3 cm/minute and the width y is increasing at the rate of 2 cm/minute. When x = 10 cm and y = 6 cm, find the rate of change of (a) the perimeter and (b) the area of rectangle

86 Views

32.

The length x of a rectangle is decreasing at the rate of 5 cm/minute and the width y is increasing at the rate of 4 cm/minutc. When x = 8 cm and y = 6 cm, find the rates of change of (a) the perimeter, and (b) the area of the rectangle.

77 Views

Long Answer Type

33.

The two equal sides of an isosceles triangle with fixed base b are decreasing at the rate of 3 cm per second. How fast is the area decreasing when the two equal sides are equal to the base?

88 Views

Short Answer Type

34.

A particle moves along the curve 6y = x³ + 2. Find the points on the curve at which the y-coordinate is changing 8 times as fast as the x-coordinate.

141 Views

Long Answer Type

35.

At what points of the ellipse 16x² + 9y² = 400, does the ordinate decrease at the same rate at which the abscissa increases?

289 Views

36.
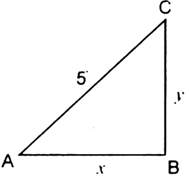
A ladder 5 m long is leaning against a wall. The bottom of the ladder is pulled along the ground, away from the wall, at the rate of 2 cm/s. How fast is its height on the wall decreasing when the foot of the ladder is 4m away from the wall?

Let the foot A of the ladder be at a distance x metres from the wall and y metres be the height of the wall at any time t.
$therefore space space space space space straight x squared plus straight y squared space equals space 25 space space space space space space space space space space space space space space space space space space space space space space... left parenthesis 1 right parenthesis$

Differentiating both sides w.r.t. 't', we get,
$2 straight x dx over dt plus 2 straight y dy over dt space equals space 0$

$rightwards double arrow space space space space space straight x dx over dt plus straight y dy over dt space equals space 0$
$But space dx over dt space equals space 2 space cm divided by straight s space space equals space space 0.02 space straight m divided by straight s space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space$ (given)
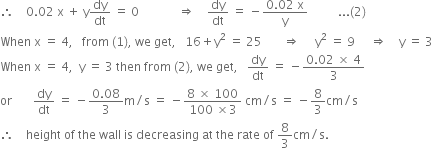
$therefore space space space space 0.02 space straight x space plus space straight y dy over dt space equals space 0 space space space space space space space space space space space space space rightwards double arrow space space space space dy over dt space equals space minus fraction numerator 0.02 space straight x over denominator straight y end fraction space space space space space space space space space space... left parenthesis 2 right parenthesis When space straight x space equals space 4 comma space space space from space left parenthesis 1 right parenthesis comma space we space get comma space space space 16 plus straight y squared space equals space 25 space space space space space space space rightwards double arrow space space space space space straight y squared space equals space 9 space space space space space rightwards double arrow space space space space straight y space equals space 3 When space straight x space equals space 4 comma space space straight y space equals space 3 space then space from space left parenthesis 2 right parenthesis comma space we space get comma space space space dy over dt space equals space minus fraction numerator 0.02 space cross times space 4 over denominator 3 end fraction or space space space space space space space dy over dt space equals space minus fraction numerator 0.08 over denominator 3 end fraction straight m divided by straight s space equals space minus fraction numerator 8 space cross times space 100 over denominator 100 space cross times 3 end fraction space cm divided by straight s space equals space minus 8 over 3 cm divided by straight s therefore space space space space height space of space the space wall space is space decreasing space at space the space rate space of space 8 over 3 cm divided by straight s.$

85 Views

Short Answer Type

37.

Sand is pouring from a pipe at the rate of 12 cm³/s. The falling sand forms a cone on the ground in such a way what the height of the cone is always one-sixth of the radius of the base. How fast is the height of the sand-cone increasing when the height is 4 cm?

78 Views

Long Answer Type

38. A water tank has the shape of an inverted right circular cone with its axis vertical and vertex lowermost. Its semi-vertical angle is tan^–1 (0.5). Water is poured into it at a constant rate of 5 cubic metre per hour. Find the rate at which the level of the water is rising at the instant when the depth of water in the tank is 4 m.

139 Views

Short Answer Type

39.

A man 2 metres high walks at a uniform speed of 6 metre/sec away from a lamp-post 6 metres high. Find the rate at which the length of his shadow increases.

77 Views

40.

A man of height 2 metres walks at a uniform speed of 5 km/h away from a lamp post which is 6 metres high. Find the rate at which the length of his shadow increases.

170 Views