Long Answer TypeWater is dripping out from a conical funnel, at the uniform rate of 2 cc/sec through a tiny hole at the vertex of the funnel. When the slant height of water is 5 cm, find the rate of decrease of the slant height of the water.
Let V be the volume of the water in the cone i.e. the volume of the water cone CA 'B' at any time t.
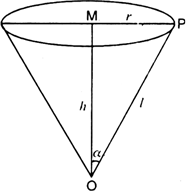
Let CO' = h, O' A' = r and CA' = I.
Let α be the semi-vertical angle of the cone. CAB where CO = 15 cm, OA = 5 cm
CO = 15 cm
OA = 5 cm
Then, 
Also, 
...(2)
From (1) and (2), we get,
...(3)
Now, 
(ii) Let A be the water surface area at any time t. Then, A = 
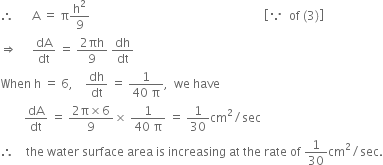
(iii) Let S be the wetted surface area of the vessel at any time t. Then. S = 
Now, 
An inverted cone has a depth of 10 cm and a base of radius 5 cm. Water is poured into it at the rate of 
Find the rate at which the level of water in the cone is rising when the depth is 4 cm.
Multiple Choice QuestionsThe total revenue in Rupees received from the sale of x units of a product is given by R(x) = 3x 2 + 36x + 5.
96
90
90
A cylindrical tank of radius 10 m is being filled with wheat at the rate of 314 cubic metre per hour. Then the depth of the wheat is increasing at the rate of
1 m3/h
Short Answer TypeShow that the tangent to the curve y = 7x3 + 11 at the points where x = 2 and x = – 2 are parallel.
Switch
