Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Application of Derivatives

Name: Zigya - For The Curious Learner
Rating: 4.4 (740 reviews)

Short Answer Type

91. Find the equation of the tangent and normal to the given curves at the points given:
y = x⁴ – 6x³ + 13x² – 10x + 5 at ( 0 , 5 )

76 Views

92. Find the equation of the tangent and normal to the given curves at the points given:
y = x⁴ –6x³+ 13x²– 10x + 5 at (1 ,3)

88 Views

93. Find the equation of the tangent and normal to the given curves at the points given:

straight y squared space equals space fraction numerator straight x cubed over denominator 4 minus straight x end fraction space space at space space left parenthesis 2 comma space space minus 2 right parenthesis

75 Views

94. Find the equation of the tangent and normal to the given curves at the points given:

straight y space equals fraction numerator 5 straight x squared over denominator 1 plus straight x squared end fraction

74 Views

Long Answer Type

95. Find the equation of the tangent and normal to the given curves at the points given:

square root of straight x plus square root of straight y space equals space 5

74 Views

96. Find the equation of the tangent and normal to the given curves at the points given:

16 straight x squared plus 9 straight y squared space equals space 144 space space space at space left parenthesis straight x subscript 1 comma space space straight y subscript 1 right parenthesis space space space where space straight x subscript 1 space equals space 2 space space space and space straight y subscript 1 greater than 0

Also find the points of intersection where both tangent and normal cut the x-axis.

80 Views

97. Find the equation of the tangent and normal to the given curves at the points given:

square root of straight x plus square root of straight y space equals space straight a space space space at space space open parentheses straight a squared over 4 comma space space straight a squared over 4 close parentheses

Also find the points of intersection where both tangent and normal cut the x-axis.

73 Views

98. Find the equation of the tangent to the curve y = (x³ – 1) (x – 2) at points where the curve cuts the x-axis.

The equation of given curve is
$straight y space equals space left parenthesis straight x cubed minus 1 right parenthesis thin space left parenthesis straight x minus 2 right parenthesis space equals space left parenthesis straight x minus 1 right parenthesis thin space left parenthesis straight x minus 2 right parenthesis thin space left parenthesis straight x squared plus straight x plus 1 right parenthesis$
It meets x-axis where y = 0
Putting y = 0, we get,
$0 space equals space left parenthesis straight x minus 1 right parenthesis thin space left parenthesis straight x minus 2 right parenthesis thin space left parenthesis straight x squared plus straight x plus 1 right parenthesis$

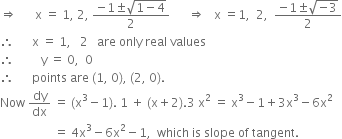
$rightwards double arrow space space space space space space straight x space equals space 1 comma space 2 comma space fraction numerator negative 1 plus-or-minus square root of 1 minus 4 end root over denominator 2 end fraction space space space space space space rightwards double arrow space space space straight x space equals 1 comma space space 2 comma space space fraction numerator negative 1 plus-or-minus square root of negative 3 end root over denominator 2 end fraction therefore space space space space space space straight x space equals space 1 comma space space space 2 space space space are space only space real space values therefore space space space space space space space space space straight y space equals space 0 comma space space 0 therefore space space space space space space points space are space left parenthesis 1 comma space 0 right parenthesis comma space left parenthesis 2 comma space 0 right parenthesis. Now space dy over dx space equals space left parenthesis straight x cubed minus 1 right parenthesis. space 1 space plus space left parenthesis straight x plus 2 right parenthesis.3 space straight x squared space equals space straight x cubed minus 1 plus 3 straight x cubed minus 6 straight x squared space space space space space space space space space space space space space space space space space space equals space 4 straight x cubed minus 6 straight x squared minus 1 comma space space which space is space slope space of space tangent.$

At (1, 0), slope of tangent = 4 (1)³ – 6 (1)²–1 = 4 – 6 – 1 = – 3
At (2, 0), slope of tangent = 4 (2)³ – 6 (2)² – 1 = 4 × 8 – 6 × 4 – 1 = 7
∴ equation of tangent at (1, 0) with slope – 3 is
y – 0 = – 3(x – 1) or y = – 3x + 3 or 3x + y – 3 = 0
The equation of tangent at (2, 0) with slope 7 is
y – 0 = 7(x – 2), or y = 7x – 14 or 7x – y - 14 = 0

78 Views

Short Answer Type

99. Find the equation of the tangent to the curve

straight y equals space fraction numerator straight x minus 7 over denominator left parenthesis straight x minus 2 right parenthesis thin space left parenthesis straight x minus 3 right parenthesis end fraction

at the point where it cuts the x-axis.

73 Views

Long Answer Type

100.

Prove that the line $straight x over straight a plus straight y over straight b space equals space 1$ is a tangent to the curve $straight y space equals be to the power of negative straight x over straight a end exponent$ at the point where the curve cuts y-axis.