Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Application of Derivatives

Name: Zigya - For The Curious Learner
Rating: 4.4 (740 reviews)

Short Answer Type

121.

Find points on the curve $straight x squared over 4 plus straight y squared over 25 space equals space 1$ at which the tangents are (i) parallel to the x-axis (ii) parallel to the y-axis.

76 Views

Long Answer Type

122.

Find points on the curve $straight x squared over 9 plus straight y squared over 16 space equals space 1$ at which the tangents are (i) parallel to the x-axis (ii) parallel to the y-axis.

82 Views

123.

For the curve y = 4x³ – 2x⁵, find all the points at which the tangent passes through the origin.

123 Views

Multiple Choice Questions

124. The points on the curve 9y² = x³, where the normal to the curve make equal intercepts with the axes are
$open parentheses 4 comma space plus-or-minus 8 over 3 close parentheses$
$open parentheses 4 comma space space minus 8 over 3 close parentheses$
$open parentheses 4 comma space plus-or-minus 3 over 8 close parentheses$
$open parentheses 4 comma space plus-or-minus 3 over 8 close parentheses$

open parentheses 4 comma space plus-or-minus 8 over 3 close parentheses

The equation of curve is $9 straight y squared space equals space straight x cubed space space space space space space space or space space space straight y squared space equals space 1 over 9 straight x cubed$ ...(1)
Differentiating both sides w.r.t.x, we get,
$2 straight y dy over dx space equals space straight x squared over 3 space space space space or space space space dy over dx space equals space fraction numerator straight x squared over denominator 6 straight y end fraction. space which space is space slope space of space tangent$
$therefore space space slope space of space normal space space equals space minus fraction numerator 6 straight y over denominator straight x squared end fraction$
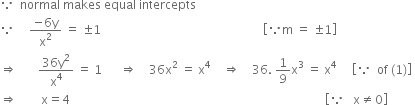
$because space space normal space makes space equal space intercepts because space space space space space fraction numerator negative 6 straight y over denominator straight x squared end fraction space equals space plus-or-minus 1 space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space open square brackets because straight m space equals space plus-or-minus 1 close square brackets rightwards double arrow space space space space space space space fraction numerator 36 straight y squared over denominator straight x to the power of 4 end fraction space equals space 1 space space space space space space rightwards double arrow space space space space 36 straight x squared space equals space straight x to the power of 4 space space space space rightwards double arrow space space space space 36. space 1 over 9 straight x cubed space equals space straight x to the power of 4 space space space space space open square brackets because space space of space left parenthesis 1 right parenthesis close square brackets rightwards double arrow space space space space space space space space straight x equals 4 space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space open square brackets because space space space straight x not equal to 0 close square brackets space space space space space space space space space$
When x =4, from (1), $straight y squared space equals space 1 over 9 cross times 64 space space space space rightwards double arrow space space space space space straight y space equals space plus-or-minus 8 over 3$
$therefore space space space space space required space points space are space open parentheses 4 comma space 8 over 3 close parentheses space and space space open parentheses 4 comma space minus 8 over 3 close parentheses$