Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Application of Derivatives

Name: Zigya - For The Curious Learner
Rating: 4.4 (740 reviews)

Short Answer Type

121.

Find points on the curve $straight x squared over 4 plus straight y squared over 25 space equals space 1$ at which the tangents are (i) parallel to the x-axis (ii) parallel to the y-axis.

76 Views

Long Answer Type

122.

Find points on the curve $straight x squared over 9 plus straight y squared over 16 space equals space 1$ at which the tangents are (i) parallel to the x-axis (ii) parallel to the y-axis.

82 Views

123.

For the curve y = 4x³ – 2x⁵, find all the points at which the tangent passes through the origin.

123 Views

Multiple Choice Questions

124. The points on the curve 9y² = x³, where the normal to the curve make equal intercepts with the axes are

$open parentheses 4 comma space plus-or-minus 8 over 3 close parentheses$
$open parentheses 4 comma space space minus 8 over 3 close parentheses$
$open parentheses 4 comma space plus-or-minus 3 over 8 close parentheses$
$open parentheses 4 comma space plus-or-minus 3 over 8 close parentheses$

124 Views

Long Answer Type

125. The curve y = ax³ + bx² + cx + 5 touches the x -axis at P (– 2, 0) and cuts the y-axis at a point Q where its gradient is 3. Find a. b, c.

123 Views

126.
Show that the curves 2x = y² and 2xy = k cut at right angles if k² = 8

The equation of two curves are
2x = y²...(1)
and    $2 xy space equals space straight k$ ...(2)
From (1) and (2), $straight y squared. space space straight y space equals space straight k space space space rightwards double arrow space space space space space straight y cubed space equals space straight k space space space space rightwards double arrow space space space straight y space equals space straight k to the power of 1 third end exponent$
$therefore space space space space from space left parenthesis 1 right parenthesis comma space space space space 2 straight x space equals space straight k to the power of 2 over 3 end exponent space space space space rightwards double arrow space space space space straight x space equals space 1 half straight k to the power of 2 over 3 end exponent$
$therefore$ point of intersection of curves (1) and (2) is $open parentheses 1 half straight k to the power of 2 over 3 end exponent comma space space straight k to the power of 1 third end exponent close parentheses$
From (1),    $2 space equals space 2 straight y dy over dx space space space space space rightwards double arrow space space space space space dy over dx space equals 1 over straight y$
$At space open parentheses 1 half straight k to the power of 2 over 3 end exponent comma space space space straight k to the power of 1 third end exponent close parentheses. space dy over dx space equals space 1 over straight k to the power of begin display style 1 third end style end exponent$
$therefore space space space space space space straight m subscript 1 space equals space 1 over straight k to the power of begin display style 1 third end style end exponent space where space straight m subscript 1 space is space slope space of space tangent space to space the space curve space left parenthesis 1 right parenthesis space at space the space point space of space intersection. space$
From (2),    $2 straight y plus 2 straight x dy over dx space equals space 0 space space space space space space rightwards double arrow space space space space dy over dx space equals space minus straight y over straight x$
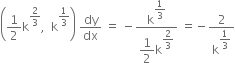
At $open parentheses 1 half straight k to the power of 2 over 3 end exponent comma space space straight k to the power of 1 third end exponent close parentheses space dy over dx space equals space minus fraction numerator straight k to the power of begin display style 1 third end style end exponent over denominator begin display style 1 half end style straight k to the power of begin display style 2 over 3 end style end exponent end fraction space equals negative 2 over straight k to the power of begin display style 1 third end style end exponent$
$therefore space space space space space straight m subscript 2 space equals space minus 2 over straight k to the power of begin display style 1 third end style end exponent space where space straight m subscript 2 space is space slope space of space tangent space to space the space curve space left parenthesis 2 right parenthesis space at space the space point space of space intersection.$
Curves (1) and (2) cut at right angles if $straight m subscript 1 straight m subscript 2 space equals space minus 1$
i.e., if $1 over straight k to the power of begin display style 1 third end style end exponent. space fraction numerator negative 2 over denominator straight k to the power of begin display style 1 third end style end exponent end fraction space equals negative 1$
i.e. if $straight k to the power of negative 2 over 3 end exponent space equals space 2 space space space space space space space space space straight i. straight e. space space space space if space space space space straight k squared space equals 8$
Hence the result.