Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Application of Derivatives

Name: Zigya - For The Curious Learner
Rating: 4.4 (740 reviews)

Multiple Choice Questions

131.

The slope of the normal to the curve y = 2 x² + 3 sin x at x = 0 is

3
$1 third$
-3
-3

84 Views

132.

The line y = x + 1 is a tangent to the curve y ² = 4x at the point

(1, 2)
(2, 3)
(1, -2)
(1, -2)

75 Views

133. The normal at the point (1, 1) on the curve 2y + x² = 3 is

x + y = 0
x – y = 0
x + y + 1 = 0
x + y + 1 = 0

114 Views

134. The normal to the curve x² = 4 y passing (1, 2) is
x + y = 3
x – y = 3
x + y = 1
x + y = 1

x + y = 3

The equation of the curve is $straight x squared space equals space 4 straight y$ ...(1)
$therefore space space space space space straight y space equals space straight x squared over 4 space space space space space space space space space rightwards double arrow space space space space dy over dx space equals space fraction numerator 2 straight x over denominator 4 end fraction space equals space straight x over 2$
Let normal at (h, k) pass through (1, 2).
Since (h, k) lies on (1)
$therefore$ $straight h squared space equals space 4 space straight k$ ...(2)
Slope of tangent at (h, k) = $straight h over 2$
$therefore space space space space slope space of space normal space at space left parenthesis straight h comma space straight k right parenthesis space equals space minus 2 over straight h$
Equation of normal at (h, k) is $straight y minus straight k space equals space minus 2 over straight h left parenthesis straight x minus straight h right parenthesis$
$because space space space space it space passes space through space left parenthesis 1 comma space 2 right parenthesis space space space space space space space space space space space space space space space therefore space space space 2 minus straight k space equals space minus 2 over straight h left parenthesis 1 minus straight h right parenthesis$
or $2 straight h minus hk space equals space minus 2 plus 2 straight h space space space space space space space space space space space space space space space space space space space space space rightwards double arrow space space space space space straight h space straight k space equals space 2$
From (2) and (3), we get, $straight h open parentheses straight h squared over 4 close parentheses space equals space 2.$
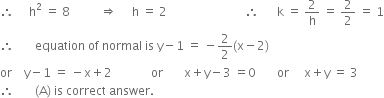
$therefore space space space space space straight h squared space equals space 8 space space space space space space space space space space rightwards double arrow space space space space space straight h space equals space 2 space space space space space space space space space space space space space space space space space space space space space space space space space space therefore space space space space space space straight k space equals space 2 over straight h space equals space 2 over 2 space equals space 1 therefore space space space space space space space equation space of space normal space is space straight y minus 1 space equals space minus 2 over 2 left parenthesis straight x minus 2 right parenthesis or space space space space straight y minus 1 space equals space minus straight x plus 2 space space space space space space space space space space space space space or space space space space space space space straight x plus straight y minus 3 space equals 0 space space space space space space space or space space space space space straight x plus straight y space equals space 3 therefore space space space space space space space left parenthesis straight A right parenthesis space is space correct space answer.$

95 Views

Short Answer Type

135. Show that the function f (x) = 2 x + 3 is a strictly increasing function on R.

85 Views

136. Without using the derivative show that the function f (a) = 7x – 3 is a strictly increasing function on R.

85 Views

137. Show that the function f (x) = x² is an increasing function in (0, ∞).

81 Views

138.

Show that the function f(x) = x² is a decreasing function in (– ∞ 0).

84 Views

139.

Construct an example of a functions which is strictly increasing but whose derivative vanishes at a point in the domain of definition of the function.

82 Views