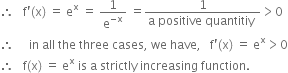Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Application of Derivatives

Name: Zigya - For The Curious Learner
Rating: 4.4 (740 reviews)

Multiple Choice Questions

131.

The slope of the normal to the curve y = 2 x² + 3 sin x at x = 0 is

3
$1 third$
-3
-3

84 Views

132.

The line y = x + 1 is a tangent to the curve y ² = 4x at the point

(1, 2)
(2, 3)
(1, -2)
(1, -2)

75 Views

133. The normal at the point (1, 1) on the curve 2y + x² = 3 is

x + y = 0
x – y = 0
x + y + 1 = 0
x + y + 1 = 0

114 Views

134. The normal to the curve x² = 4 y passing (1, 2) is

x + y = 3
x – y = 3
x + y = 1
x + y = 1

95 Views

Short Answer Type

135. Show that the function f (x) = 2 x + 3 is a strictly increasing function on R.

85 Views

136. Without using the derivative show that the function f (a) = 7x – 3 is a strictly increasing function on R.

85 Views

137. Show that the function f (x) = x² is an increasing function in (0, ∞).

81 Views

138.

Show that the function f(x) = x² is a decreasing function in (– ∞ 0).

84 Views

139.

Construct an example of a functions which is strictly increasing but whose derivative vanishes at a point in the domain of definition of the function.

82 Views

140.
Prove that the exponential function e^x is strictly increasing on R.

Let f (x) = e^x ∴ D_f = R
We are to prove that function f (x) = e^x is strictly increasing. Here interval is not given. So we will prove that function e^x is strictly increasing in its domain.
Now f ' (x) = e^xThree cases arise:
Case I.
$straight x greater than 0$
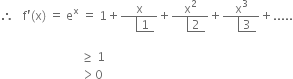
$Syntax error from line 1 column 415 to line 1 column 518. Unexpected '<mlongdiv '.$

Case II.
x = 0
∴ f ' (x) = e^x = I > 0
Case III.
$straight x less than 0$
$therefore space space space straight f apostrophe left parenthesis straight x right parenthesis space equals space straight e to the power of straight x space equals space 1 over straight e to the power of negative straight x end exponent space equals fraction numerator 1 over denominator straight a space positive space quantitiy space end fraction greater than 0 therefore space space space space space in space all space the space three space cases comma space we space have comma space space space straight f apostrophe left parenthesis straight x right parenthesis space equals space straight e to the power of straight x greater than 0 therefore space space space straight f left parenthesis straight x right parenthesis space equals space straight e to the power of straight x space is space straight a space strictly space increasing space function.$