Short Answer TypeFind the intervals in which the following functions are strictly increasing or strictly decreasing:
2x3 – 8x2 + 10x + 5
Let f (x) – 2x3 – 8x2 + 10x + 5
∴ f ' (x) = 6x2– 16x + 10 = 2 (3x2 – 8x + 5) = 2 (x – 1) (3x – 5)
For f (x) to be increasing,
f ' (x) > 0 ⇒ 2 (x – 1) (3x – 5) > 0 ⇒ (x – 1) (3 x – 5) > 0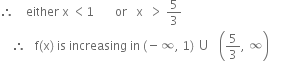
For f(x) to be decreasing,
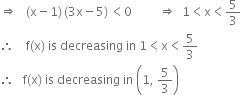
Find the intervals in which the following functions are strictly increasing or strictly decreasing:
2x3 – 6x2 – 48x + 17
Find the intervals in which the following functions are strictly increasing or strictly decreasing:
f (x) = 2x3 – 9x2 + 12x + 30
Find the intervals in which the following functions are strictly increasing or strictly decreasing:
f (x) = 2x3 – 3x2 – 36x + 7
Find the intervals in which the following functions are strictly increasing or strictly decreasing:
f(x) = 2x3 – 21x2 + 36x – 40
Find the intervals in which the following functions are strictly increasing or strictly decreasing:
4x3 – 6x2 – 72x + 30
Find the intervals in which the following functions are strictly increasing or strictly decreasing:
– 2x3 – 9x2 – 12x + 1
Long Answer TypeDetermine for which values of x, the function f (x) = x4 – 2x2 is increasing or decreasing.
Switch
, is
