 Multiple Choice Questions
Multiple Choice QuestionsThe sides of an equilateral triangle are increasing at the rate of 2 cm/s. The rate at which the area increases, when the side is 10 cm, is:
10 sq cm/s
If PQ and PR are the two sides of a triangle, then the angle between them which gives maximum area of the triangle, is :
If the volume of a sphere is increasing at a constant rate, then the rate at which its radius is increasing, is
a constant
proportional to the radius
inversely proportional to the radius
inversely proportional to the surface area
Twenty two metres are available to fence a flower bed in the form of a circular sector. If the flower bed should have the greatest possible surface area, the radius of the circle must be :
4 m
3 m
6 m
5 m
The value of x for which the polynomial 2x3 - 9x2 + 12x + 4 is a decreasing function of x, is :
- 1 < x < 1
0 < x < 2
x > 3
1 < x < 2
The length of the longest size rectangle of maximum area that can be inscribed in a semicircle of radius 1, so that 2 vertices lie on the diameter, is :
2
A.
Let the length and breadth of the rectangle be l and b.
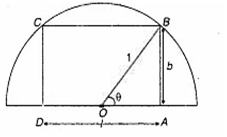
On differentiating w.r.t. , we get
Put for maxima or minima
