 Multiple Choice Questions
Multiple Choice QuestionsIf two sides of a triangle are given, then the area of the triangle will be maximum, if. the angle between the given sides is
If f(x) = , then the points of local maxima for the function f(x) are
1, 3
- 3, 1
- 1, 3
- 1, - 3
The adjacent sides of a rectangle with given parameter as 200 cm and enclosing minimum area are
20 cm and 80 cm
50 cm and 50 cm40 cm and 60 cm
50 cm and 50 cm
30 cm and 70 cm
The altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius r is
Let f(x) = x(x - 1)2, the point at which f(x) assumes maximum and minimum are respectively
3, 1
None of these
Rectangles are inscribed ina circle of radius r. The dimensions of the rectangle which has the maximum area, are
r, r
2r, 2r
None of the above
C.
Let ABCD be the rectangle inscribed in a circle of radius r.
Let AB = x
and BC = y
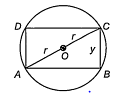
Then, x2 + y2 = 4r2
Let P(x) = a0 + a1x2 + a2x2 + a3x6 + ... + anx2n be a polynomial in a real variables with 0 < a0 < a1 < a2 < .... < an. The function P(x) has
neither a maxima nor a minima
only one maxima
both maxima and minima
only one minima
The equation of tangent of the curve y = be-x/a at the point, where the curve meet y-axis is
bx + ay - ab = 0
ax + by - ab = 0
bx - ay - ab = 0
ax + by - ab = 0
If y = 4x - 5 is a tangent to the curve y2 = px3 + q at (2, 3), then
p = 2, q = - 7
p = - 2, q = 7
p = - 2, q = - 7
p = 2, q = 7
