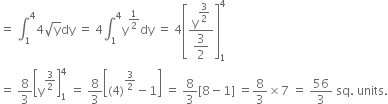Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Application of Integrals

Short Answer Type

1. Find the area of the region bounded by the curve y²= x and the lines x = 1, x = 4 and the x-axis in the first quadrant.

953 Views

Find the area of the region bounded by y² = 4 x, x = 1, x = 4 and the x-axis in the first quadrant.

821 Views

3. Find the area of the region bounded by y² = 9x, x = 2, x = 4 and the x-axis in the first quadrant.

752 Views

Find the area of the region bounded by y² = x - 2, x = 4, x = 6 and the x-axis in the first quadrant.

610 Views

5. Find the area under the given curves and given lines:
(i) y = x², x = 1, x = 2 and x-axis
(ii) y - x^4, x = 1, x = 5 and x -axis

422 Views

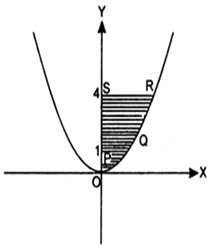
Find the area of the region bounded by x² = 4 y, y = 2, y = 4 and the y-axis in the first quadrant.

275 Views

7. Find the area of the region lying in the first quadrant and bounded by y = 4 x², x = 0, y = 1 and y = 4.

164 Views

8. Find the area of the region lying in the first quadrant and bounded by x² = y - 3, y = 4, y = 6 and the y-axis in the first quadrant.

333 Views

9.
Find the area of the region bounded by x² = 16 y, y = 1, y = 4 and the y-axis in the first quadrant.

Name: Zigya - For The Curious Learner
Rating: 4.4 (740 reviews)

The equation of curve is
$straight x squared space equals space 16 space straight y$
Required area = $integral subscript 1 superscript 4 straight x space dy$
$equals space integral subscript 1 superscript 4 4 square root of straight y dy space equals space 4 integral subscript 1 superscript 4 straight y to the power of 1 half end exponent dy space equals space 4 open square brackets fraction numerator straight y to the power of begin display style 3 over 2 end style end exponent over denominator begin display style 3 over 2 end style end fraction close square brackets subscript 1 superscript 4 equals space 8 over 3 open square brackets straight y to the power of 3 over 2 end exponent close square brackets subscript 1 superscript 4 space equals space 8 over 3 open square brackets left parenthesis 4 right parenthesis to the power of 3 over 2 end exponent minus 1 close square brackets space equals space 8 over 3 left square bracket 8 minus 1 right square bracket space equals 8 over 3 cross times 7 space equals space 56 over 3 space sq. space units.$