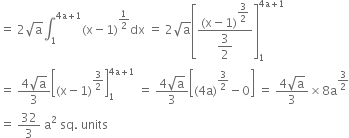Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

1. Find the area of the region bounded by the curve y²= x and the lines x = 1, x = 4 and the x-axis in the first quadrant.

953 Views

Find the area of the region bounded by y² = 4 x, x = 1, x = 4 and the x-axis in the first quadrant.

821 Views

3. Find the area of the region bounded by y² = 9x, x = 2, x = 4 and the x-axis in the first quadrant.

752 Views

Find the area of the region bounded by y² = x - 2, x = 4, x = 6 and the x-axis in the first quadrant.

610 Views

5. Find the area under the given curves and given lines:
(i) y = x², x = 1, x = 2 and x-axis
(ii) y - x^4, x = 1, x = 5 and x -axis

422 Views

Find the area of the region bounded by x² = 4 y, y = 2, y = 4 and the y-axis in the first quadrant.

275 Views

7. Find the area of the region lying in the first quadrant and bounded by y = 4 x², x = 0, y = 1 and y = 4.

164 Views

8. Find the area of the region lying in the first quadrant and bounded by x² = y - 3, y = 4, y = 6 and the y-axis in the first quadrant.

333 Views

Find the area of the region bounded by x² = 16 y, y = 1, y = 4 and the y-axis in the first quadrant.

317 Views

Name: Zigya - For The Curious Learner
Rating: 4.4 (740 reviews)

The equation of parabola is y² = 4 a (x-1) ...(1)
When y = 4 a , from (1) 16 a² = 4 a (x-1)
⇒ x - 1 = 4 a ⇒ x = 4 a + 1

therefore space space required space area space equals space integral subscript straight x space equals space 1 end subscript superscript straight x equals 4 straight a plus 1 end superscript straight y space dx space equals space integral subscript straight x equals 1 end subscript superscript straight x space equals space 4 straight a plus 1 end superscript 2 square root of straight a space square root of straight x minus 1 end root space dx

open square brackets because space of space left parenthesis 1 right parenthesis close square brackets

equals space 2 square root of straight a integral subscript 1 superscript 4 straight a plus 1 end superscript left parenthesis straight x minus 1 right parenthesis to the power of 1 half end exponent dx space equals space 2 square root of straight a open square brackets fraction numerator left parenthesis straight x minus 1 right parenthesis to the power of begin display style 3 over 2 end style end exponent over denominator begin display style 3 over 2 end style end fraction close square brackets subscript 1 superscript 4 straight a plus 1 end superscript equals space fraction numerator 4 square root of straight a over denominator 3 end fraction open square brackets left parenthesis straight x minus 1 right parenthesis to the power of 3 over 2 end exponent close square brackets subscript 1 superscript 4 straight a plus 1 end superscript space equals space fraction numerator 4 square root of straight a over denominator 3 end fraction open square brackets left parenthesis 4 straight a right parenthesis to the power of 3 over 2 end exponent minus 0 close square brackets space equals space fraction numerator 4 square root of straight a over denominator 3 end fraction cross times 8 straight a to the power of 3 over 2 end exponent equals space 32 over 3 space straight a squared space sq. space units

315 Views