Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Application of Integrals

Name: Zigya - For The Curious Learner
Rating: 4.4 (740 reviews)

Long Answer Type

21.

Draw a graph of $straight x squared over 9 plus straight y squared over 25 space equals space 1$ and evaluate area bounded by it.

121 Views

22. Using definite integrals, find the area of the ellipse $straight x squared over 4 plus straight y squared over 9 space equals space 1$

The equation of the ellipse is
$straight x squared over 4 plus straight y squared over 9 space equals space 1$
or $straight y squared over 9 space equals space 1 minus straight x squared over 4$
or $straight y squared space equals space 9 over 4 left parenthesis 4 minus straight x squared right parenthesis$

$therefore space space space space straight y space equals space 3 over 2 square root of 4 minus straight x squared end root$ ...(1)
(in the first quadrant)
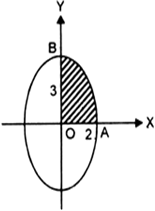
The ellipse is symmetrical about both the axes,
∴ required area = 4 (area AOB)
$equals space 4 integral subscript 0 superscript 2 straight y space dx space equals space 4 space integral subscript 0 superscript 2 3 over 2 square root of 4 minus straight x squared end root dx$ $open square brackets because space of space left parenthesis 1 right parenthesis close square brackets$
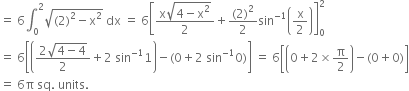
$equals space 6 integral subscript 0 superscript 2 square root of left parenthesis 2 right parenthesis squared minus straight x squared end root space dx space equals space 6 open square brackets fraction numerator straight x square root of 4 minus straight x squared end root over denominator 2 end fraction plus fraction numerator left parenthesis 2 right parenthesis squared over denominator 2 end fraction sin to the power of negative 1 end exponent open parentheses straight x over 2 close parentheses close square brackets subscript 0 superscript 2 equals space 6 open square brackets open parentheses fraction numerator 2 square root of 4 minus 4 end root over denominator 2 end fraction plus 2 space sin to the power of negative 1 end exponent 1 close parentheses minus left parenthesis 0 plus 2 space sin to the power of negative 1 end exponent 0 right parenthesis close square brackets space equals space 6 open square brackets open parentheses 0 plus 2 cross times straight pi over 2 close parentheses minus left parenthesis 0 plus 0 right parenthesis close square brackets equals space 6 straight pi space sq. space units.$

148 Views

23.

Draw a graph of $straight x squared over 9 plus fraction numerator straight y squared over denominator 16 space end fraction space equals space 1$ and evaluate area bounded by it.

112 Views

Short Answer Type

24.

Using definite integrals, find the area of the ellipse $straight x squared over straight a squared plus straight y squared over straight b squared equals 1$ .

259 Views

25.

Sketch the region of the ellipse and find its area, using integration.
$straight x squared over straight b squared plus straight y squared over straight a squared equals 1.$

135 Views

Long Answer Type

26. Find the area of the region in the first quadrant enclosed by the x-axis, the line

straight x equals square root of 3 space straight y

and the circle x² + y² = 4.

155 Views

27. Find the area of the region in the first quadrant enclosed by the x-axis, the line y = x, and the circle x² + y² = 32.

637 Views

28.

Find the area bounded by the ellipse $straight x squared over straight a squared plus straight y squared over straight b squared equals 1 space and space the space$ ordinates x = a e and x = 0 where b² = a² (1 - e²) and e < 1.

286 Views

Short Answer Type

29. Find the area of the region bounded by the parabola y = x² + 1 and the lines y = x, x = 0 and x = 2.

153 Views

Long Answer Type

30. Find the area of the region bounded by the curves y = x² + 2, y = x, x = 0 and x = 3.

150 Views