 Long Answer Type
Long Answer Type Short Answer Type
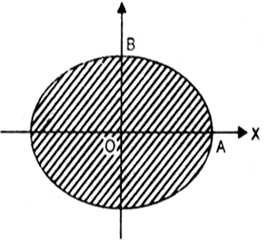
Short Answer TypeUsing definite integrals, find the area of the ellipse ![]() .
.
The equation of the ellipse is![]() ...(1)
...(1)
The ellipse is symmetrical about the axes.
∴ required area = 4 (area OAB)![]() [
[![]() ]
]![]()
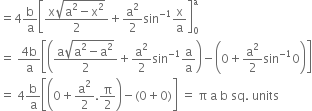
 Long Answer Type
Long Answer TypeFind the area bounded by the ellipse ![]() ordinates x = a e and x = 0 where b2 = a2 (1 - e2) and e < 1.
ordinates x = a e and x = 0 where b2 = a2 (1 - e2) and e < 1.
 Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type