Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Application of Integrals

Name: Zigya - For The Curious Learner
Rating: 4.4 (740 reviews)

Long Answer Type

21.

Draw a graph of $straight x squared over 9 plus straight y squared over 25 space equals space 1$ and evaluate area bounded by it.

121 Views

22. Using definite integrals, find the area of the ellipse

straight x squared over 4 plus straight y squared over 9 space equals space 1

148 Views

23.

Draw a graph of $straight x squared over 9 plus fraction numerator straight y squared over denominator 16 space end fraction space equals space 1$ and evaluate area bounded by it.

112 Views

Short Answer Type

24.

Using definite integrals, find the area of the ellipse $straight x squared over straight a squared plus straight y squared over straight b squared equals 1$ .

259 Views

25.

Sketch the region of the ellipse and find its area, using integration.
$straight x squared over straight b squared plus straight y squared over straight a squared equals 1.$

135 Views

Long Answer Type

26. Find the area of the region in the first quadrant enclosed by the x-axis, the line $straight x equals square root of 3 space straight y$ and the circle x² + y² = 4.

The equation of circle is
$straight x squared plus straight y squared space equals space 4$ ...(1)
The equation of line is
   $straight x space equals square root of 3 space straight y$ ...(2)
From (1) and (2), we get,
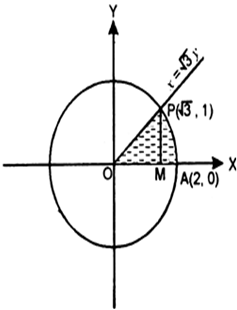
   $3 straight y squared plus straight y squared space equals space 4 space space space space or space space space space 4 straight y squared space equals space 4$
$therefore space space space space space space space space straight y squared space equals space 1 rightwards double arrow space space space space space space straight y space equals space 1 space space space space space space space space space rightwards double arrow space space space space space straight x space equals space square root of 3$

∴ point of intersection of circle (1) and line (2) is P $left parenthesis square root of 3 comma space 1 right parenthesis$ .
From P, draw PM ⊥ x-axis.
Also OA = radius of circle = 2
∴ A is (2, 0)
Required area = Area OMAPO = Area of ∆OMP + area MAP
= A₁ + A₂    ..(1 )
where $straight A subscript 1 space equals space area space of space increment OMP space equals space fraction numerator 1 over denominator square root of 3 end fraction integral subscript 0 superscript square root of 3 end superscript space straight x space dx$

equals space fraction numerator 1 over denominator square root of 3 end fraction open square brackets straight x squared over 2 close square brackets subscript 0 superscript square root of 3 end superscript space equals space left parenthesis 1 right parenthesis space fraction numerator 1 over denominator 2 square root of 3 end fraction left parenthesis 3 minus 0 right parenthesis space equals space fraction numerator square root of 3 over denominator 2 end fraction

and

straight A subscript 2 space equals space integral subscript square root of 3 end subscript superscript 2 space straight y space dx space equals space integral subscript square root of 3 end subscript superscript 2 square root of 4 minus straight x squared end root space dx space equals space integral subscript square root of 3 end subscript superscript 2 square root of left parenthesis 2 right parenthesis squared minus straight x squared end root space dx

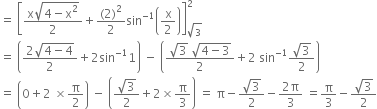
equals space open square brackets fraction numerator straight x square root of 4 minus straight x squared end root over denominator 2 end fraction plus fraction numerator left parenthesis 2 right parenthesis squared over denominator 2 end fraction sin to the power of negative 1 end exponent open parentheses straight x over 2 close parentheses close square brackets subscript square root of 3 end subscript superscript 2 equals space open parentheses fraction numerator 2 square root of 4 minus 4 end root over denominator 2 end fraction plus 2 sin to the power of negative 1 end exponent 1 close parentheses space minus space open parentheses fraction numerator square root of 3 space square root of 4 minus 3 end root over denominator 2 end fraction plus 2 space sin to the power of negative 1 end exponent fraction numerator square root of 3 over denominator 2 end fraction close parentheses equals space open parentheses 0 plus 2 space cross times straight pi over 2 close parentheses space minus space open parentheses fraction numerator square root of 3 over denominator 2 end fraction plus 2 cross times straight pi over 3 close parentheses space equals space straight pi minus fraction numerator square root of 3 over denominator 2 end fraction minus fraction numerator 2 straight pi over denominator 3 end fraction space equals straight pi over 3 minus fraction numerator square root of 3 over denominator 2 end fraction

therefore space space from space left parenthesis 1 right parenthesis comma space required space area space equals space fraction numerator square root of 3 over denominator 2 end fraction plus straight pi over 3 minus fraction numerator square root of 3 over denominator 2 end fraction equals space straight pi over 3 space sq. space units

155 Views

27. Find the area of the region in the first quadrant enclosed by the x-axis, the line y = x, and the circle x² + y² = 32.

637 Views

28.

Find the area bounded by the ellipse $straight x squared over straight a squared plus straight y squared over straight b squared equals 1 space and space the space$ ordinates x = a e and x = 0 where b² = a² (1 - e²) and e < 1.