Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Application of Integrals

Name: Zigya - For The Curious Learner
Rating: 4.4 (740 reviews)

Long Answer Type

21.

Draw a graph of $straight x squared over 9 plus straight y squared over 25 space equals space 1$ and evaluate area bounded by it.

121 Views

22. Using definite integrals, find the area of the ellipse

straight x squared over 4 plus straight y squared over 9 space equals space 1

148 Views

23.

Draw a graph of $straight x squared over 9 plus fraction numerator straight y squared over denominator 16 space end fraction space equals space 1$ and evaluate area bounded by it.

112 Views

Short Answer Type

24.

Using definite integrals, find the area of the ellipse $straight x squared over straight a squared plus straight y squared over straight b squared equals 1$ .

259 Views

25.

Sketch the region of the ellipse and find its area, using integration.
$straight x squared over straight b squared plus straight y squared over straight a squared equals 1.$

135 Views

Long Answer Type

26. Find the area of the region in the first quadrant enclosed by the x-axis, the line

straight x equals square root of 3 space straight y

and the circle x² + y² = 4.

155 Views

27. Find the area of the region in the first quadrant enclosed by the x-axis, the line y = x, and the circle x² + y² = 32.

637 Views

28.

Find the area bounded by the ellipse $straight x squared over straight a squared plus straight y squared over straight b squared equals 1 space and space the space$ ordinates x = a e and x = 0 where b² = a² (1 - e²) and e < 1.

286 Views

Short Answer Type

29. Find the area of the region bounded by the parabola y = x² + 1 and the lines y = x, x = 0 and x = 2.

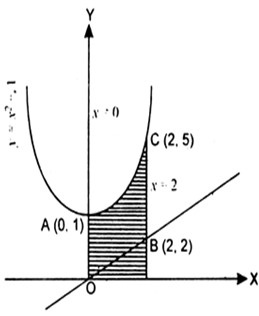
We are to find the area of the region bounded by the curves.
   $straight y space equals space straight x squared plus 1 comma straight y space equals space straight x comma straight x space equals space 0$
and x = 2
Now    $straight y space equals space straight x squared plus 1$ is an upward parabola with vertex A (0, 1), y =x is straight line passing through the origin, B(2, 2) and lies below the parabola.
Now area bounded by the parabola, above the x-axis and ordinates x = 0, x = 2.
   $equals space integral subscript 0 superscript 2 left parenthesis straight x squared plus 1 right parenthesis space dx space equals space open square brackets straight x cubed over 3 plus straight x close square brackets subscript 0 superscript 2 space equals space open parentheses 8 over 3 plus 2 close parentheses space minus space left parenthesis 0 plus 0 right parenthesis space equals space 14 over 3$
Area bounded by the line y = x, above the x-axis and ordinates x = 0, x = 2.
   $equals space integral subscript 0 superscript 2 straight x space dx space equals space open square brackets straight x squared over 2 close square brackets subscript 0 superscript 2 space equals space 4 over 2 minus 0 space equals space 2$

   $therefore space required space area space equals space 14 over 3 minus 2 space equals space 8 over 3 space sq. space units.$