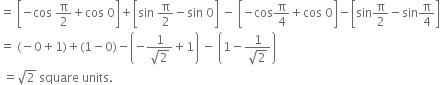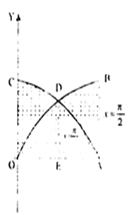Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Application of Integrals

Name: Zigya - For The Curious Learner
Rating: 4.4 (740 reviews)

Long Answer Type

31. Find the area of the region enclosed by the parabola y² = 4 a x and the line y = mx.

176 Views

32.

Find the area bounded by the curve y = x² and the line y = x.
OR
Find the area of the region {(x. y): x² ≤ y ≤ x}.

202 Views

33. Using the method of integration find the area bounded by the curve |x| + |y| = 1.
[Hint: The required region is bounded by lines x + y = 1, x– y = 1, – x + y = 1 and
– x – y = 1].

146 Views

34.

Find the area of the region bounded by the line y = 3 x + 2, the x-axis and the ordinates x = - 1 and x = 1.

112 Views

35. Find the area of the region included between the parabola

straight y space equals 3 over 4 straight x squared space and space the space line space 3 straight x space minus space 2 straight y space plus space 12 space equals space 0

127 Views

36. Find the area bounded by the parabola x² = 4 y and the straight line x = 4 y - 2.

201 Views

37. Find the area of the region included between the parabola y² = x and the line x + y = 2.

1184 Views

38.

Find the area of the region enclosed by the parabola x² = y, the line y = x + 2 and the x-axis.
OR
Draw the rough sketch and find the area of the region:
{(x, y): x² < y < x + 2}

518 Views

Short Answer Type

39.
Draw a rough sketch of the curves y = sin x and y = cos x as x varies from 0 to $straight pi over 2$ and find the area of the region enclosed by them and the x-axis.

Let OB and CA represent the curves y = sin x and y = cos x as x varies from 0 to $straight pi over 2$ . The two curves intersect at D where
   $sinx space equals space cosx space space space space space space space space space space rightwards double arrow space space space tanx space equals space 1 space space space space space space space space space space rightwards double arrow space space straight x space equals space straight pi over 4$
Required area = Area OAB + area OCA - area ODA
$equals space integral subscript 0 superscript straight pi over 2 end superscript sinx space dx space plus space integral subscript 0 superscript straight pi over 2 end superscript cosx space dx minus integral subscript 0 superscript straight pi over 4 end superscript sinx space dx space minus integral subscript straight pi over 4 end subscript superscript straight pi over 2 end superscript cosx space dx$

   $equals open square brackets negative cos space straight x space close square brackets subscript 0 superscript straight pi over 2 end superscript plus open square brackets sin space straight x close square brackets subscript 0 superscript straight pi over 2 end superscript minus open square brackets negative cos space straight x close square brackets subscript 0 superscript straight pi over 4 end superscript space minus space open square brackets sin space straight x close square brackets subscript straight pi over 4 end subscript superscript straight pi over 2 end superscript$    $equals space open square brackets negative cos space straight pi over 2 plus cos space 0 close square brackets plus open square brackets sin space straight pi over 2 minus sin space 0 close square brackets space minus space open square brackets negative cos straight pi over 4 plus cos space 0 close square brackets minus open square brackets sin straight pi over 2 minus sin straight pi over 4 close square brackets equals space left parenthesis negative 0 plus 1 right parenthesis plus left parenthesis 1 minus 0 right parenthesis minus open parentheses negative fraction numerator 1 over denominator square root of 2 end fraction plus 1 close parentheses space minus space open parentheses 1 minus fraction numerator 1 over denominator square root of 2 end fraction close parentheses space equals square root of 2 space square space units.$