 Short Answer Type
Short Answer Type Long Answer Type
Long Answer TypeUsing integration, find the area of the triangular region whose sides have the equationsВ y = 2 x + 1,В y = 3 x + 1В and x = 4.
The equations of the sides are
y = 2 x + 1 В В В ...(1)
y = 3 x + 1 В В В ...(2)
and x = 4. В В В ...(3)
Subtracting (1) from (2), we get,
В В В В В В В В В ![]()
Putting x = 0 В in (1), we get y = 0+1 = 1![]() В В line (1) and (2) intersect in A(0, 1)
В В line (1) and (2) intersect in A(0, 1)
From (1) and (3), we get,
В В В В В В В В В В В ![]()
![]() В line (1) and (3) intersect in B (4, 9)
В line (1) and (3) intersect in B (4, 9)
From (2) and (3), we get,
x = 4, y = 12 + 1 = 13
∴  lines (2) and (3) intersect in C (4, 13)
∴ vertices of the triangle ABC are A(0, 1), B (4, 9), C (4, 13)
Required area = Area of ∆ ABC = Area of region AOMC - area of region AOMB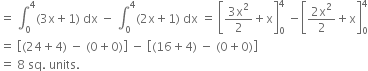
Using integration, find the area of the region bounded by the triangle whose vertices are (-1, 1), (0, 5) and (3, 2).
 Short Answer Type
Short Answer TypeUsingВ integration, find the area of the region bounded by the triangle whose vertices areВ (1, 0), (2, 2) and (3, 1).
 Long Answer Type
Long Answer TypeUsingВ integration find the area of region bounded by the triangle whose vertices are (-1, 0), (1, 3) and (3, 2).
