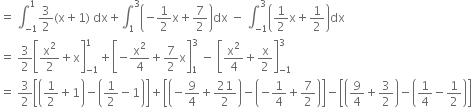Short Answer Type
Short Answer Type Long Answer Type
Long Answer TypeUsing integration, find the area of the triangular region whose sides have the equationsВ y = 2 x + 1,В y = 3 x + 1В and x = 4.
Using integration, find the area of the region bounded by the triangle whose vertices are (-1, 1), (0, 5) and (3, 2).
 Short Answer Type
Short Answer TypeUsingВ integration, find the area of the region bounded by the triangle whose vertices areВ (1, 0), (2, 2) and (3, 1).
 Long Answer Type
Long Answer TypeUsingВ integration find the area of region bounded by the triangle whose vertices are (-1, 0), (1, 3) and (3, 2).
Let A(-1, 0), B(1, 3), C(3, 2) be the vertices of the given triangle.В
The equation of AB is
В В В В В В В В В В ![]()
or В В В В В В В В В ![]() В В В В В В В ...(1)
В В В В В В В ...(1)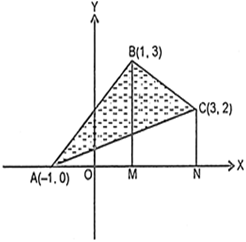
The equation of BC is
В В В В В В В В В В В ![]()
or В В В В В В В В ![]()
or В В В В В В В В В ![]() В В В В В В В В В В В В ...(2)
В В В В В В В В В В В В ...(2)
The equation of CA is
В В В В В В В В В В ![]()
or В В В В В ![]() В В В В В ...(3)
В В В В В ...(3)
From B, drawВ BM вЉҐ x-axis and from C, draw CN вЉҐ x-axis.
Required area = Area of ∆ABC
= Area ofВ ![]() В + area of region BMNC - area ofВ
В + area of region BMNC - area ofВ ![]()