 Long Answer Type
Long Answer Type Short Answer Type
Short Answer TypeThe equations of curves are
![]() ...(1)
...(1)
and ![]() ...(2)
...(2)
From (2), ![]() ...(3)
...(3)
Putting this value of y in (1),
![]()
or ![]()
![]()
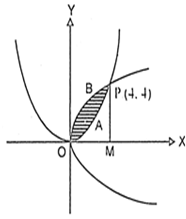
From P, draw PM ![]() x-axis.
x-axis.
Required area = Area OAPB
= Area OBPM - area OAPM
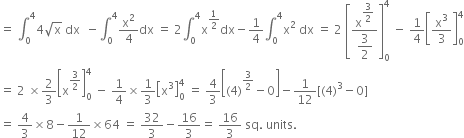
 Long Answer Type
Long Answer Type Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type