 Long Answer Type
Long Answer Type Short Answer Type
Short Answer Type Long Answer Type
Long Answer TypeThe equations of curves are
В В В В В В В В В В В В В В ![]() В В В В В В В В В В В В В В В В В В В В В В В ...(1)
В В В В В В В В В В В В В В В В В В В В В В В ...(1)
В В and В В В В В В В В В ![]() В В В В В В В В В В В В В В В В В В В В В В ...(2)
В В В В В В В В В В В В В В В В В В В В В В ...(2)
В В From (1) and (2), we get
В В В В В В В В В ![]()


![]() В В curves (1) and (2) intersect in O(0, 0), P(9, 9)
В В curves (1) and (2) intersect in O(0, 0), P(9, 9)
В В В From P, drawВ ![]() В x-axis.В
В x-axis.В
В В В Required area = Area OAPBO = Area OBPM - area OAPM
В В В В В В В В В В В В В В В В ![]()
В В В 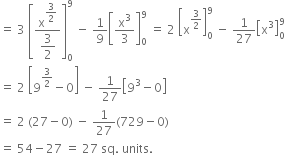
 Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type