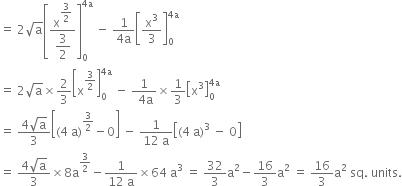Long Answer Type
Long Answer Type Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type Short Answer Type
Short Answer Type Long Answer Type
Long Answer TypeThe equations of curves are
В В В В В В В В В В ![]() В В В В В В В В В В ...(1)
В В В В В В В В В В ...(1)
and В В В В В В В ![]() В В В В В В В В В В ...(2)
В В В В В В В В В В ...(2)
From (2),В ![]() В В В В В В В В В В В В В ...(3)
В В В В В В В В В В В В В ...(3)
Putting this value of y in (1),![]()
or В В В В В В В В ![]()
∴ x = 0, 4 a
∴ from (3), y = 0, 4 a
∴ curves (1) and (2) intersect in O (0, 0), P (4 a, 4 a).
From P. draw PM вЉҐ x-axis.
Required area = Area OAPB
= Area OBPM - area OAPM![]()
В