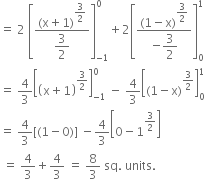Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Application of Integrals

Name: Zigya - For The Curious Learner
Rating: 4.4 (740 reviews)

Long Answer Type

51. Find the area of the region enclosed between the two circles x² + y² = 4 and (x - 2)² + y² = 4.

892 Views

52. Find the area of the region enclosed between the two circles x² + y² = 1 and (x - 1)² + y² = 1.

565 Views

53. Find the area of the region enclosed between the two circles x² + y² = 1 and

open parentheses straight x minus 1 half close parentheses squared plus straight y squared space equals space 1.

156 Views

Short Answer Type

54. Find the area of the region bounded by two parabola 4 y = x² and 4 x = y²

136 Views

Long Answer Type

55. Find the area included between the two curves y² = 9x and ,x² = 9y. Also draw the rough sketch.

398 Views

Short Answer Type

56.

Calculate the area of the region bounded by the y = x² and x = y².

100 Views

Long Answer Type

57. Draw a graph of y² = 16 x and x² = 16y, and evaluate the area between them.

192 Views

58. Find the area of the region included between the parabolas y² = 4 a x and x² = 4 a y, a > 0.

185 Views

59. Draw the rough sketch of y² = x + 1 and y² = - x + 1 and determine the area enclosed by the two curves.

The equation of given curves are
y² - x + 1    ...(1)
and    y² = -x + 1    ...(2)
From (1) and (2), we get,
x + 1 = -x + 1 ⇒ 2 x = 0 ⇒ x = 0
Putting x = 0 in (1). we get,
y² = 1 or y = -1, 1
∴ points of intersection of given curves are (0, -1) and (0, 1).
Now (1) and (2) represent two parabolas having vertices at (-1, 0) and (1, 0).
Required area = 2 [area CAO + area OBC]
$equals space 2 open square brackets integral subscript negative 1 end subscript superscript 0 square root of straight x plus 1 end root dx plus integral subscript 0 superscript 1 square root of straight x minus 1 end root dx close square brackets$
   $equals space 2 space open square brackets fraction numerator left parenthesis straight x plus 1 right parenthesis to the power of begin display style 3 over 2 end style end exponent over denominator begin display style 3 over 2 end style end fraction close square brackets subscript negative 1 end subscript superscript 0 plus 2 open square brackets fraction numerator left parenthesis 1 minus straight x right parenthesis to the power of begin display style 3 over 2 end style end exponent over denominator negative begin display style 3 over 2 end style end fraction close square brackets subscript 0 superscript 1 equals space 4 over 3 open square brackets open parentheses straight x plus 1 close parentheses to the power of 3 over 2 end exponent close square brackets subscript negative 1 end subscript superscript 0 space minus space 4 over 3 open square brackets left parenthesis 1 minus straight x right parenthesis to the power of 3 over 2 end exponent close square brackets subscript 0 superscript 1 equals space 4 over 3 left square bracket left parenthesis 1 minus 0 right parenthesis right square bracket space minus 4 over 3 open square brackets 0 minus 1 to the power of 3 over 2 end exponent close square brackets space equals space 4 over 3 plus 4 over 3 space equals space 8 over 3 space sq. space units. space$