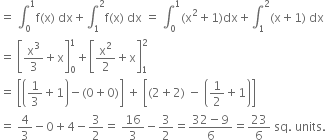The given region is
{( x, y): 0 ≤ y ≤ x² + 1, 0 ≤ y ≤ x + 1, 0 ≤ x ≤ 2}
Thus region is the intersection of the following regions:
R₁ = {(x, y) : 0 ≤ y ≤ x² + 1}
R₂ = { (x, y) : 0 ≤ y ≤ x + 1}
R₃ = {(x, y) : 0 ≤ x ≤ 2}
The function with graph in the figure is

Consider the equations
y = x² + 1    ...(1)
and y = x + 1    ...(2)
Putting y = x + 1 in (1), we get
x + 1 = x² + 1, or x = x² ⇒ x² - x = 0 ⇒ x(x - 1) = 0
∴ x = 0, 1
∴ from (2), y = 1, 2
∴ curve (1) and (2) intersect in the points P (0, 1) and Q (1, 2).
The region considered is bounded by
                              y = f(x),
                              y = 0
                              x = 0
              and          x = 2
 required area =