Short Answer Type
Short Answer Type Long Answer Type
Long Answer TypeFind the area of the region bounded by the circle x2 + y2 = 1 and x + y = 1. Also draw a rough sketch.
Find the area of the region {(x, y): x2 ≤ y ≤ |x|}.
Or
Find the area of the region bounded by the parabola y = x2 and y = |x|.
The equation of circle is
x2 + y2 = 8 x ...(1)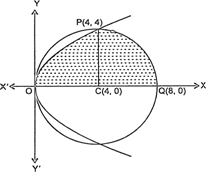
The equation of parabola is
y2 = 4 x ...(2)
(1) can be written as
(x2 - 8 x) + y2 = 0 or (x2 - 8 x + 16) + y2 = 16
or (x - 4)2 + y2 = (4)2 ...(3)
which is a circle with centre C(4, 0) and radius = 4.
From (1) and (2), we get,
x2 + 4 x = 8 x or x2 - 4 x = 0 ⇒ x(x - 4) = 0
∴ x = 0, 4
∴ from (2), y =0, 4
∴ points of intersection of circle (1) and parabola (2) and 0(0, 0) and P(4, 4), above the x-axis.
Required area = area of region OPQCO
= (area of region OCPO) + (area of region PCQP)