 Long Answer Type
Long Answer TypeUsing integration, find the area of the smaller region bounded by the curve ![]() and the straight line
and the straight line ![]()
Let I = ![]()
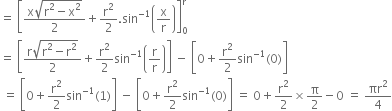
Let ![]()
Now ![]()
![]()
![]()
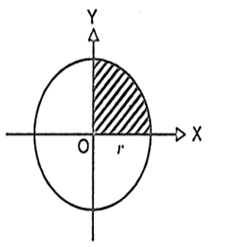
![]() represents the area bounded by the circle
represents the area bounded by the circle ![]() the x-axis and the ordinate x = 0 and the ordinate x = r, i.e., it represents the area of the region in the first quadrant.
the x-axis and the ordinate x = 0 and the ordinate x = r, i.e., it represents the area of the region in the first quadrant. ![]()
 Short Answer Type
Short Answer Type Multiple Choice Questions
Multiple Choice Questions