 Multiple Choice Questions
Multiple Choice Questions-9
0
 Long Answer Type
Long Answer TypeThe equation of curves are
В В В В В В В В В В В В В В В В ![]() В В В В В В В В В В ...(1)
В В В В В В В В В В ...(1)
В В В В В В В В В and В В В ![]() В В В В В В В В В ...(2)
В В В В В В В В В ...(2)
From (2), В ![]() В В В В В В В В В В В В В В В В В ...(3)
В В В В В В В В В В В В В В В В В ...(3)
Putting this value of y in (1),![]()
or В В ![]()
![]()
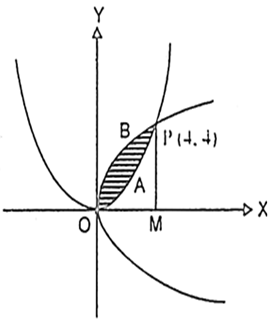
From P. draw PM вЉҐ x-axis.
Required area = Area OAPB = Area OBPM - area OAPM
В В В В В В В В В В В В В 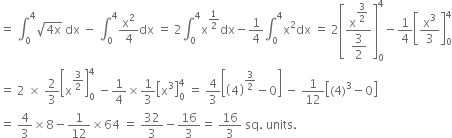
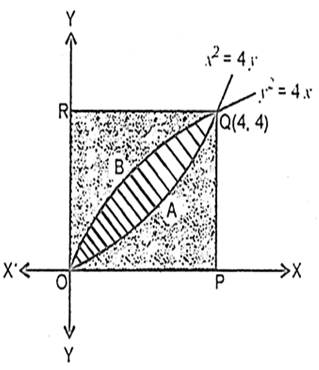
Now, the area of the region OAQBO bounded by curvesВ ![]() В andВ
В andВ ![]()
В В В В В В В В В В В В В В В В В 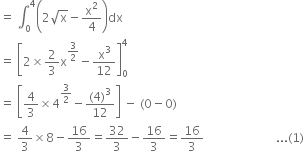
Again, the area of the region OPQAO bounded by the curves x2В = 4 y, x = 0, x = 4 and x-axis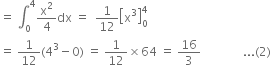
Similarly, the area of the region OBQRO bounded by the curveВ ![]()
![]() В В ...(3)
В В ...(3)
From (1), (2) and (3), it is clear that the area of the region OAQBO = area of the region OPQAO = area of the region OBQRO, i.e., urea bounded by parabolas y2В = 4 x and x2В = 4 y divides the area of the square in three equal parts.
Using the method of integration, find the area of the triangular region whose vertices are (2, -2), (4, 3) and (1, 2).
Using integration, find the area of the region bounded by the triangle whose vertices are (-1, 2), (1, 5) and (3, 4).
Using integration, find the area bounded by the curve x2 = 4y and the line x = 4y – 2.
