Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Application of Integrals

Name: Zigya - For The Curious Learner
Rating: 4.4 (740 reviews)

Multiple Choice Questions

81.

Area lying between the curves y² = 4x and y = 2x is

$2 over 3$
$1 third$
$1 fourth$
$1 fourth$

196 Views

82. Area bounded by the curve y = x³ the x-axis and the ordinates x - 2 and a = 1 is

-9
$fraction numerator negative 15 over denominator 4 end fraction$
$15 over 4$
$15 over 4$

110 Views

83. The area bounded by the curve y = x |x|, x-axis and the ordinates x = - 1 and x = 1 is given by

0
$1 third$
$2 over 3$
$2 over 3$

122 Views

84. The area of the circle x +y =16 exterior to the parabola y² = 6x is

$4 over 3 left parenthesis 4 straight pi minus square root of 3 right parenthesis$
$4 over 3 left parenthesis 4 straight pi plus square root of 3 right parenthesis$
$4 over 3 left parenthesis 8 straight pi minus square root of 3 right parenthesis$
$4 over 3 left parenthesis 8 straight pi minus square root of 3 right parenthesis$

196 Views

85.

The area bounded by the x-axis, y = cosx and y = sin x when $0 less or equal than straight x less or equal than straight pi over 2$

$2 left parenthesis square root of 2 minus 1 right parenthesis$
$square root of 2 minus 1$
$square root of 2 plus 1$
$square root of 2 plus 1$

162 Views

Long Answer Type

86. Prove that the curves y² = 4x and x² = 4y divide the area of the square bounded by x = 0, x = 4, y = 4 and y = 0 into three equal parts.

640 Views

87.

Using the method of integration, find the area of the triangular region whose vertices are (2, -2), (4, 3) and (1, 2).

1133 Views

88.
Sketch the region bounded by the curves $straight y equals square root of 5 minus straight x squared end root space and space straight y space equals open vertical bar straight x minus 1 close vertical bar$ and find its area using integration.

Consider the given equation.
$straight y equals square root of 5 minus straight x squared end root$
This equation represents a semicircle with centre at the origin and radius = $square root of 5 space units$
Given that the region is bounded by the above semicircle and the line $straight y equals open vertical bar straight x minus 1 close vertical bar$
Let us find the point of intersection of the given curve meets the line $straight y equals open vertical bar straight x minus 1 close vertical bar$
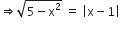
$rightwards double arrow square root of 5 minus straight x squared end root space equals space open vertical bar straight x minus 1 close vertical bar$
Squaring both the sides, we have,

$5 minus straight x squared space equals open vertical bar straight x minus 1 close vertical bar squared rightwards double arrow 5 minus straight x squared space equals space straight x squared plus 1 minus 2 straight x rightwards double arrow 2 straight x squared minus 2 straight x minus 5 plus 1 space equals space 0 rightwards double arrow 2 straight x squared minus 2 straight x minus 4 space equals space 0 rightwards double arrow straight x squared minus straight x minus 2 space equals 0 rightwards double arrow space straight x squared minus 2 straight x plus straight x minus 2 space equals 0 rightwards double arrow straight x left parenthesis straight x minus 2 right parenthesis plus 1 left parenthesis straight x minus 2 right parenthesis equals 0 rightwards double arrow left parenthesis straight x plus 1 right parenthesis thin space left parenthesis straight x minus 2 right parenthesis space equals space 0 rightwards double arrow straight x space equals negative 1 comma space straight x space equals space 2 When space straight x space equals space minus 1 comma space space straight y space equals space 2 When space straight x space equals space 2 comma space space straight y space equals space 1$
Consider the following figure
Thus the intersection points are 1,2 and 2,1 ( ) ( ) Consider the following sketch of the bounded region.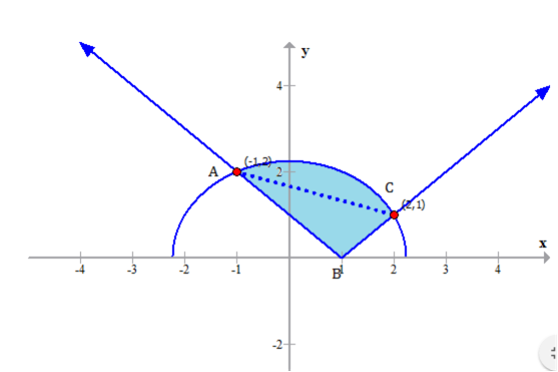

Required Area, $straight A space equals space integral subscript negative 1 end subscript superscript 2 left parenthesis straight y subscript 2 minus straight y subscript 1 right parenthesis dx space$
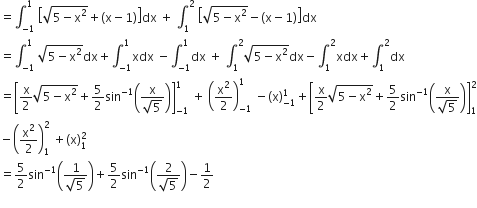
$equals integral subscript negative 1 end subscript superscript 1 space open square brackets square root of 5 minus straight x squared end root plus left parenthesis straight x minus 1 right parenthesis close square brackets dx space plus space integral subscript 1 superscript 2 space open square brackets square root of 5 minus straight x squared end root minus left parenthesis straight x minus 1 right parenthesis close square brackets dx equals integral subscript negative 1 end subscript superscript 1 space square root of 5 minus straight x squared end root dx plus integral subscript negative 1 end subscript superscript 1 xdx space minus integral subscript negative 1 end subscript superscript 1 dx space plus space integral subscript 1 superscript 2 square root of 5 minus straight x squared end root dx minus integral subscript 1 superscript 2 xdx plus integral subscript 1 superscript 2 dx equals open square brackets straight x over 2 square root of 5 minus straight x squared end root plus 5 over 2 sin to the power of negative 1 end exponent open parentheses fraction numerator straight x over denominator square root of 5 end fraction close parentheses close square brackets subscript negative 1 end subscript superscript 1 space plus space open parentheses straight x squared over 2 close parentheses subscript negative 1 end subscript superscript 1 space minus left parenthesis straight x right parenthesis subscript negative 1 end subscript superscript 1 plus open square brackets straight x over 2 square root of 5 minus straight x squared end root plus 5 over 2 sin to the power of negative 1 end exponent open parentheses fraction numerator straight x over denominator square root of 5 end fraction close parentheses close square brackets subscript 1 superscript 2 minus open parentheses straight x squared over 2 close parentheses subscript 1 superscript 2 space plus left parenthesis straight x right parenthesis subscript 1 superscript 2 equals 5 over 2 sin to the power of negative 1 end exponent open parentheses fraction numerator 1 over denominator square root of 5 end fraction close parentheses plus 5 over 2 sin to the power of negative 1 end exponent open parentheses fraction numerator 2 over denominator square root of 5 end fraction close parentheses minus 1 half$

$Required space Area space equals open square brackets 5 over 2 sin to the power of negative 1 end exponent open parentheses fraction numerator 1 over denominator square root of 5 end fraction close parentheses plus 5 over 2 sin to the power of negative 1 end exponent open parentheses fraction numerator 2 over denominator square root of 5 end fraction close parentheses minus 1 half close square brackets sq. space units$