Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Areas Related to Circles

Short Answer Type

1. The radii of two circles are 19 cm and 9 cm respectively. Find the radius of the circle which has circumference equal to the sum of the circumference of two circles.

1620 Views

2. The radii of two circles are 8 cm and 6 cm respectively. Find the radius of the circle having its area equal to the sum of the areas of the two circles.

1153 Views

Long Answer Type

3. Fig. 12.3, depicts an archery target marked with its five scoring areas from the centre outwards as Gold, Red, Blue, Black and White. The diameter of the region representing Gold score is 21 cm and each of the other bands is 10.5 cm wide. Find the area of each of the five scoring regions.

Fig. 12.3

977 Views

Short Answer Type

4. The wheels of a car are of diameter 80 cm each. How many complete revolutions does each wheel make in 10 minutes when the car is travelling at a speed of 66 km per hour?

986 Views

Tick the correct answer in the following: If the perimeter and the area of a circle are numerically equal, then the radius of the circle is
(A) 2 units (D) π units
(C) 4 units (D) 7 units.

707 Views

6. Find the area of a sector of a circle with radius 6 cm and of angle 60°.

214 Views

7. Find the area of a quadrant of a circle whose circumference is 22 cm.

164 Views

8. The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in 5 minutes.

425 Views

9.
A chord of circle of radius 10 cm subtends a right angle at the centre. Find the area of the corresponding :

(i) Minor segment
(ii) Major sector.

Here, we have
r = 10 cm, and ө = 90°

Here, we haver = 10 cm, and ө = 90°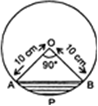Area of sector (OAPBO)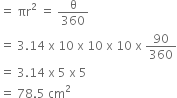Area of

Area of sector (OAPBO)

$equals space πr squared space equals space straight theta over 360 equals space 3.14 space straight x space 10 space straight x space 10 space straight x space 10 space straight x space 90 over 360 equals space 3.14 space straight x space 5 space straight x space 5 equals space 78.5 space cm squared$

Area of $increment$ AOB

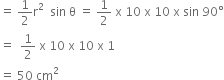
$equals space 1 half straight r squared space space sin space straight theta space equals space 1 half space straight x space 10 space straight x space 10 space straight x space sin space 90 degree equals space space 1 half space straight x space 10 space straight x space 10 space straight x space 1 equals space 50 space cm squared$

Now,
(i) Let APB A is the given minor segment, then Area of minor segment (APBA)
= Area of sector (OAPBO) - area of ∆ (AOB)
= 78.5 cm² - 50 cm²= 28.5 cm².
(ii) Area of major sector
= Area of circle Area of sector OAPBO
= (πr² - 78.5) cm²= (3.14 × 10 × 10 - 78.5) cm²= (314 - 78.5) cm² = 235.5 cm²

1110 Views

10.

In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find :

(i)    the length of the arc
(ii)    area of the sector formed by the arc
(iii)    area of the segment formed by the corresponding chord.

274 Views

Previous Year Papers

Test Series

Test Yourself

Short Answer Type

Long Answer Type

Short Answer Type

9. A chord of circle of radius 10 cm subtends a right angle at the centre. Find the area of the corresponding : (i) Minor segment(ii) Major sector.

9.
A chord of circle of radius 10 cm subtends a right angle at the centre. Find the area of the corresponding :

(i) Minor segment
(ii) Major sector.