 Short Answer Type
Short Answer Type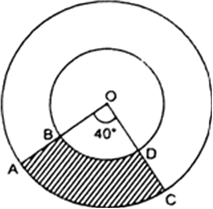
Find the area of the shaded region in Fig. 12.21, if ABCD is a square of side 14 cm and APD and BPC are semicircles.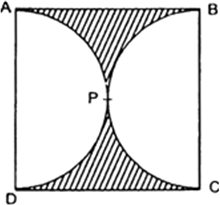
Fig. 12.21.

From each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in Fig. 12.23. Find the area of the remaining portion of the square. 
Fig. 12.23
 Long Answer Type
Long Answer TypeIn a circular table cover of radius 32 cm, a design is formed leaving an equilateral triangle ABC in the middle as shown in Figure. Find the area of the design
 Short Answer Type
Short Answer Type
Fig. 12.26 depicts a racing track whose left and right ends are semicircular.
Fig. 12.26
The distance between the two inner parallel line segments is 60 m and they are each 106 m long. If the track is 10 m wide, find :
(i) the distance around the track along its inner edge.
(ii) the area of the track.
We have,
The distance between the two inner parallel line segments = 60 m.
Length of each parallel lines = 106 m.
Width of track = 10 m
(i) The distance around the track along its inner edge = sum of length of inner parallel lines + 2 (semi perimeter of inner circular ends)
= (106 + 106) + 2 ![]()
= ![]()
(ii) OD = 30 m and AD = 10 m.
Oa = OD + DA = 30 + 10 = 40 m
Area of the track = Area of rectangle ABCD + Area of rectangle EFGH + 2 (Area of semicircle with radius 40 m - Area of semi-circle with radius 30)
= 106 x 10 + 106 x 10 + 2 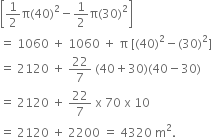
Hence, the area of track is 4320 m2
In Fig. 12.27, AB and CD are two diameters of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region.
 Long Answer Type
Long Answer TypeThe area of an equilateral triangle ABC is 17320.5 cm2 . With each vertex of the triangle as centre, a circle is drawn with radius equal to half the length of the side of the triangle (see Fig. 12.28). Find the area of the shaded region (Use ![]() = 3.14 and
= 3.14 and ![]() 1.73205)
1.73205)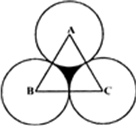
Fig. 12.28
 Short Answer Type
Short Answer TypeOn a square handkerchief, nine circular designs each of radius 7 cm are made (see Fig. 12.29). Find the area of the remaining portion of the handkerchief.
Fig. 12.29
