Short Answer Type
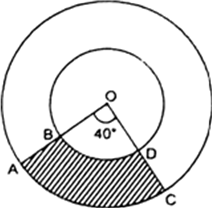
Find the area of the shaded region in Fig. 12.21, if ABCD is a square of side 14 cm and APD and BPC are semicircles.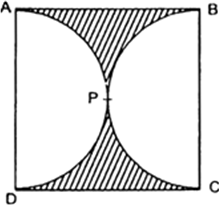
Fig. 12.21.
From each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in Fig. 12.23. Find the area of the remaining portion of the square. 
Fig. 12.23
Long Answer TypeIn a circular table cover of radius 32 cm, a design is formed leaving an equilateral triangle ABC in the middle as shown in Figure. Find the area of the design
Short Answer Type
Fig. 12.26 depicts a racing track whose left and right ends are semicircular.
Fig. 12.26
The distance between the two inner parallel line segments is 60 m and they are each 106 m long. If the track is 10 m wide, find :
(i) the distance around the track along its inner edge.
(ii) the area of the track.
In Fig. 12.27, AB and CD are two diameters of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region.
Long Answer TypeThe area of an equilateral triangle ABC is 17320.5 cm2 . With each vertex of the triangle as centre, a circle is drawn with radius equal to half the length of the side of the triangle (see Fig. 12.28). Find the area of the shaded region (Use 
= 3.14 and 
1.73205)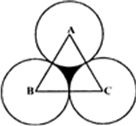
Fig. 12.28
Short Answer TypeOn a square handkerchief, nine circular designs each of radius 7 cm are made (see Fig. 12.29). Find the area of the remaining portion of the handkerchief.
Fig. 12.29
Radius of a circle = 7cm Length of side of the square = 3 (diameter)
= 3 (14) = 42 cm.
Area of the square = side2 = 422 = 1764 cm2
Area of one circle = 
Area of a circle = 9 × 154 = 1386 cm2
Remaining portion (without design)= Area of the handkerchief - Area of design
= 1764 - 1386 = 378 cm2
Hence, the area of the remaining portion is 378 cm2.
Switch
