 Long Answer Type
Long Answer Type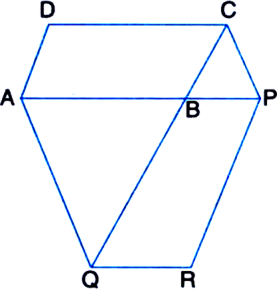
 Short Answer Type
Short Answer TypeIn figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that
(i) ar(ΔACB) = ar(ΔACF)
(ii) ar(□AEDF) = ar(ABCDE). 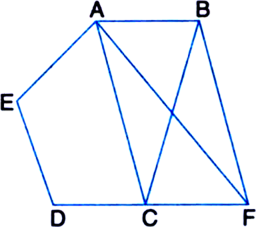
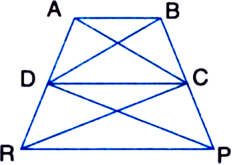
Show that the area of a rhombus is half the product of the lengths of its diagonals.
Or
Prove that the area of a rhombus is equal to half the rectangle contained by its diagonals.
