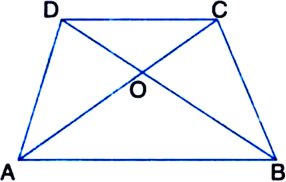
Short Answer Type
Short Answer Type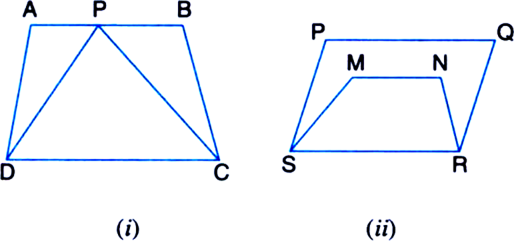
(i) ΔPDC and quadrilateral ABCD lie on the same base DC and between the same parallels DC and AB.
(iii) ΔTRQ and parallelogram SRQP lie on the same base RQ and between the same parallels RQ and SP.
(v) Quadrilaterals APCD and ABQD lie on the same base AD and between the same parallels AD and BQ.
 Long Answer Type
Long Answer TypeIf E, F, G and H are respectively the mid-points of the sides of a parallelogram ABCD, show that ar(EFGH) = ![]() ar(ABCD).
ar(ABCD).
 Short Answer Type
Short Answer Type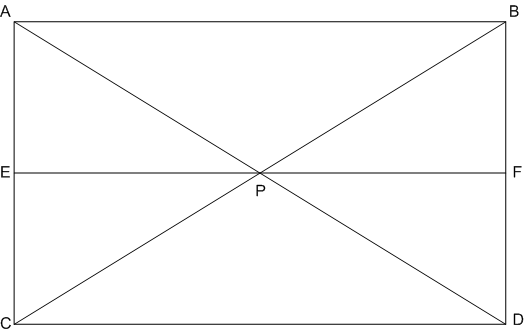
[Hint. Through P, draw a line parallel to AB.]
 Long Answer Type
Long Answer TypeIn figure, PQRS and ABRS are parallelograms and X is any point on side BR. Show that: 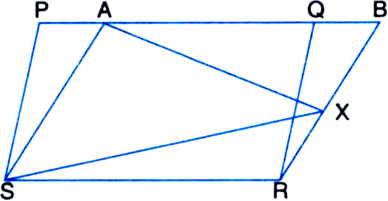
(i) ar(|| gm PQRS) = ar(|| gm ABRS)
(ii) ![]()
 Short Answer Type
Short Answer Type