Short Answer Type
Short Answer Type
 Long Answer Type
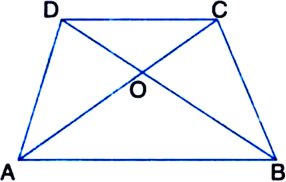
Long Answer TypeIf E, F, G and H are respectively the mid-points of the sides of a parallelogram ABCD, show that ar(EFGH) = ![]() ar(ABCD).
ar(ABCD).
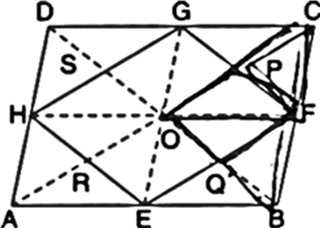
ar(ABCD).
Construction: Join OF, OG, OH and OE. Also, join AC and BD.
Proof: In ΔBCD,
∵ F and G are the mid-points of BC and DC respectively.
∴ FG || BD ...(1)
In a triangle, the line segment joining the mid-points of any two sides is parallel to the third side
In ΔBAD,
∵ E and H are the mid-points of AB and AD respectively.
EH || BD ...(2)
In a triangle, the line segment joining the mid-points of any two sides is parallel to the third side
From (1) and (2),
EH || FG ...(3)
Similarly, we can prove that
EF || HG ...(4)
From (3) and (4),
Quadrilateral EFGH is a parallelogram
| A quadrilateral is a parallelogram if its opposite sides are equal
∵ F is the mid-point of CB and O is the mid-point of CA
FO || BA
In a triangle, the line segment joining the mid-points of any two sides is parallel to the third side and is half of it ⇒ FO || CG ...(5)
V BA || CD (opposite sides of a parallelogram are parallel)
∴ BA || CG
and 
∵ Opposite sides of a parallelogram are equal = CG ...(6)
| ∵ G is the mid-point of CD In view of (5) and (6),
Quadrilateral OFCG is a parallelogram
∵ A quadrilateral is a parallelogram if a pair of opposite sides are parallel and are of
equal length
∵ OP = PC
| ∵ Diagonals of a || gm bisect each other
∵ ΔOPF and ∵CPF have equal bases
(∵ OP = PC) and have a common vertex F Their altitudes are also the same ar(ΔOPF) = ar(ΔCPF)
Similarly, ar(ΔOQF) = ar(ΔBQF)
Adding, we get
ar(ΔOPF) + ar(ΔOQF) = ar(ΔCPF) + ar(ΔBQF) ⇒ ar(|| gm OQFP) = ar(ΔCPF) + ar(ΔBQF) ....(7)
Similarly,
ar(|| gm OPGS) = ar(⇒GPC) + ar(⇒DSG) ...(8)
ar(|| gm OSHR) = ar(ΔDSH) + ar(ΔHAR)
ar(|| gm OREQ) = ar(ΔARE) + ar(ΔEQB) ...(10)
Adding the corresponding sides of (7), (8), (9) and (10), we get
ar(|| gm EFGH) = {ar(ACPF} + ar(ΔGPC)}
+ {ar(ΔDSG) + ar(ΔDSH)} + {ar(ΔHAR) + ar(ΔARE)} + (ar(ΔBQF) + ar(ΔEQB)}
= ar(ΔFCG) + ar(ΔGDH) + ar(ΔHAE) + ar(ΔEBF)![]()
 Short Answer Type
Short Answer Type
[Hint. Through P, draw a line parallel to AB.]
 Long Answer Type
Long Answer TypeIn figure, PQRS and ABRS are parallelograms and X is any point on side BR. Show that: 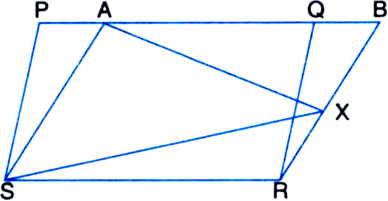
(i) ar(|| gm PQRS) = ar(|| gm ABRS)
(ii) ![]()
 Short Answer Type
Short Answer Type