Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Areas of Parallelograms and Triangles

Short Answer Type

1. Which of the following figures lie on the same base and between the same parallels. In such a case, write the common base and the two parallels.

1120 Views

2. In figure, ABCD is a parallelogram, AE ⊥ DC and CF ⊥ AD. If AB = 16 cm, AE = 8 cm and CF = 10 cm, find AD.

3027 Views

Long Answer Type

If E, F, G and H are respectively the mid-points of the sides of a parallelogram ABCD, show that ar(EFGH) = $1 half$ ar(ABCD).

1737 Views

Short Answer Type

4. P and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar(ΔAPB) = ar{ΔBQC).

920 Views

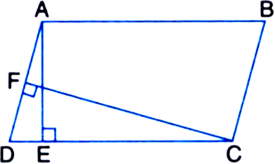
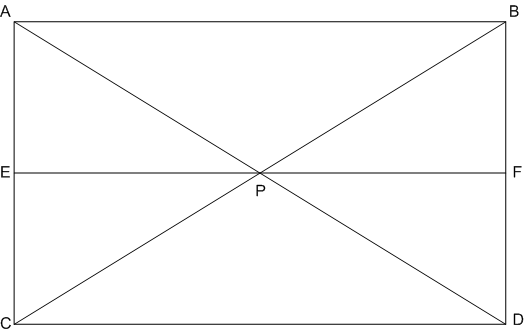
5. In figure, P is a point in the interior of a parallelogram ABCD. Show that:

(1) ar(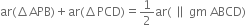 $ar left parenthesis increment APB right parenthesis plus ar left parenthesis increment PCD right parenthesis equals 1 half ar left parenthesis space parallel to space gm space ABCD right parenthesis$
(ii) ar(ΔAPD) + ar(ΔPBC) = ar(ΔAPB) + ar(ΔPCD). [CBSE 2012 (March)]
[Hint. Through P, draw a line parallel to AB.]

Given: P is a point in the interior of a parallelogram ABCD.

To Prove : (i)

ar left parenthesis increment APB right parenthesis plus ar left parenthesis increment PCD right parenthesis equals 1 half

ar(|| gm ABCD)
(ii) ar(ΔAPD) + ar(ΔPBC) = ar(ΔAPB) + ar(ΔPCD).
Construction: Through P, draw a line EF parallel to AB.

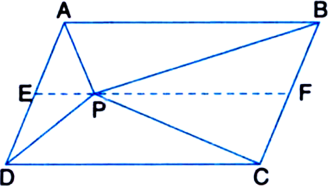
Given: P is a point in the interior of a parallelogram ABCD.To Prove

Given: P is a point in the interior of a parallelogram ABCD.To Prove

Proof: (i) EF || AB ...(1) | by construction
∵ AD || BC
∵ Opposite sides of a parallelogram are parallel
∴ AE || BF ...(2)
In view of (1) and (2),
Quadrilateral ABFE is a parallelogram
A quadrilateral is a parallelogram if its opposite sides are parallel
Similarly, quadrilateral CDEF is a parallelogram
∵ ΔAPB and || gm ABFE are on the same base AB and between the same parallels AB and EF.

therefore space space ar left parenthesis increment APB right parenthesis equals 1 half ar left parenthesis space parallel to space gm space ABFE right parenthesis space space space space space space space space space space space... left parenthesis 3 right parenthesis

∵ ΔPCD and || gm CDEF are on the same base DC and between the same parallels DC and EF.

therefore space space space space space space ar left parenthesis increment PCD right parenthesis space equals space 1 half ar left parenthesis space parallel to space gm space CDEF right parenthesis space space space space space space space space space space space space space space... left parenthesis 4 right parenthesis

Adding (3) and (4), we get ar(ΔAPB) + ar(ΔPCD)

equals space 1 half ar left parenthesis space parallel to space gm space ABFE right parenthesis plus 1 half ar space left parenthesis parallel to space gm space CDEF right parenthesis equals space 1 half left square bracket space ar space parallel to space gm space ABFE right parenthesis plus ar space left parenthesis space parallel to space gm space CDEF right parenthesis right square bracket equals space 1 half ar left parenthesis space parallel to space gm space ABCD right parenthesis space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space... left parenthesis 5 right parenthesis

(ii) ar(ΔAPD) + ar(ΔPBC)
= ar(|| gm ABCD) – [ar(ΔAPB) + ar(ΔPCD)] = 2 [ar(ΔAPB) + ar(ΔPCB)] – [ar(ΔAPB) + ar(ΔPCD)]
= ar(ΔAPB) + ar(ΔPCD).

1556 Views

Long Answer Type

In figure, PQRS and ABRS are parallelograms and X is any point on side BR. Show that:

(i) ar(|| gm PQRS) = ar(|| gm ABRS)

(ii) $ar left parenthesis increment AXS right parenthesis equals 1 half ar left parenthesis space parallel to space gm space PQRS right parenthesis.$

356 Views

Short Answer Type

7. A farmer was having a field in the form of a parallelogram PQRS. She took any point A on RS and joined it to points P and Q. In how many parts the fields is divided? What are the shapes of these parts? The farmer wants to sow wheat and pulses in equal portions of the field separately. How should she do it?

256 Views

8. The diagonals of a parallelogram ABCD intersect at a point O. Through O, a line is drawn to intersect AD at P and BC at Q. Show that PQ divides the parallelogram into two parts of equal area.

4000 Views