Short Answer Type
Short Answer Type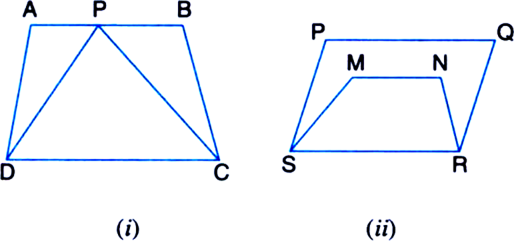
 Long Answer Type
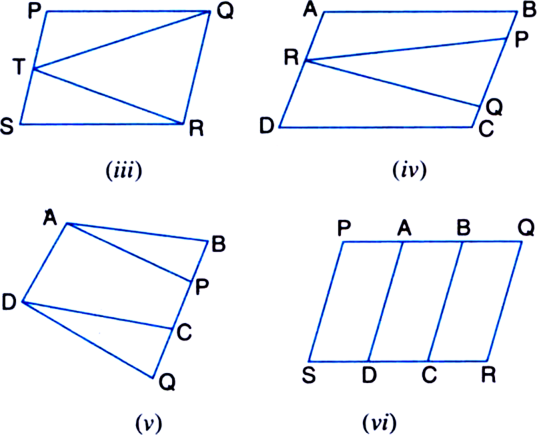
Long Answer TypeIf E, F, G and H are respectively the mid-points of the sides of a parallelogram ABCD, show that ar(EFGH) = ![]() ar(ABCD).
ar(ABCD).
 Short Answer Type
Short Answer Type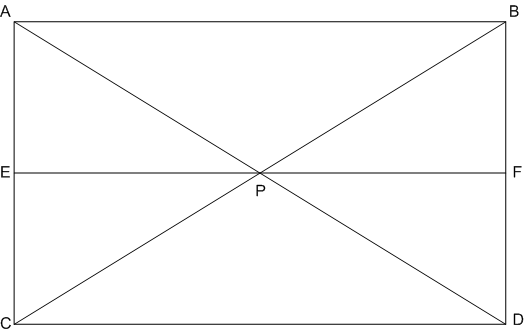
[Hint. Through P, draw a line parallel to AB.]
 Long Answer Type
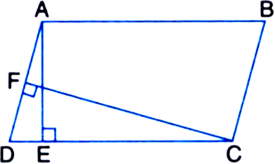
Long Answer TypeIn figure, PQRS and ABRS are parallelograms and X is any point on side BR. Show that: 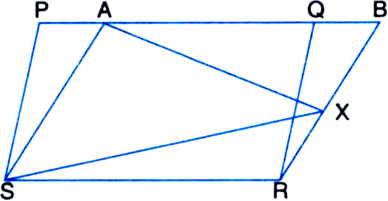
(i) ar(|| gm PQRS) = ar(|| gm ABRS)
(ii) ![]()
Given: PQRS and ABRS are parallelograms and X is any point on side BR.
To Prove: (i) ar(|| gm PQRS) = ar(|| gm ABRS)
(ii) ![]()
Proof: (i) In ΔPSA and ΔQRB,
∠SPA = ∠RQB ...(1)
Corresponding angles from PS || QR and transversal PB
∠PAS = ∠QBR ...(2)
Corresponding angles from AS || BR and transversal PB
∠PSA = ∠QRB ...(3)
| Angle sum property of a triangle Also, PS = QR ...(4)
| Opposite sides of || gm PQRS In view of (1), (3) and (4),
ΔPSA ≅ ΔQRB ...(5)
| By ASA Rule ∴ ar(ΔPSA) = ar(ΔQRB) ...(6)
| ∴ Congruent figures have equal areas Now, ar(|| gm PQRS) = ar(ΔPSA)
+ ar(|| gm AQRS) = ar(ΔQRB) + ar(|| gm AQRS)
| Using (6)
= ar(|| gm ABRS)
(ii) ∵ ΔAXS and || gm ABRS are on the same base AS and between the same parallels AS and BR.
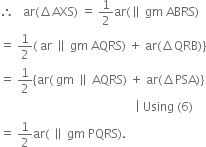
 Short Answer Type
Short Answer Type