Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Areas of Parallelograms and Triangles

Short Answer Type

1. Which of the following figures lie on the same base and between the same parallels. In such a case, write the common base and the two parallels.

1120 Views

2. In figure, ABCD is a parallelogram, AE ⊥ DC and CF ⊥ AD. If AB = 16 cm, AE = 8 cm and CF = 10 cm, find AD.

3027 Views

Long Answer Type

If E, F, G and H are respectively the mid-points of the sides of a parallelogram ABCD, show that ar(EFGH) = $1 half$ ar(ABCD).

1737 Views

Short Answer Type

4. P and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar(ΔAPB) = ar{ΔBQC).

920 Views

5. In figure, P is a point in the interior of a parallelogram ABCD. Show that:

(1) ar(

ar left parenthesis increment APB right parenthesis plus ar left parenthesis increment PCD right parenthesis equals 1 half ar left parenthesis space parallel to space gm space ABCD right parenthesis

(ii) ar(ΔAPD) + ar(ΔPBC) = ar(ΔAPB) + ar(ΔPCD). [CBSE 2012 (March)]

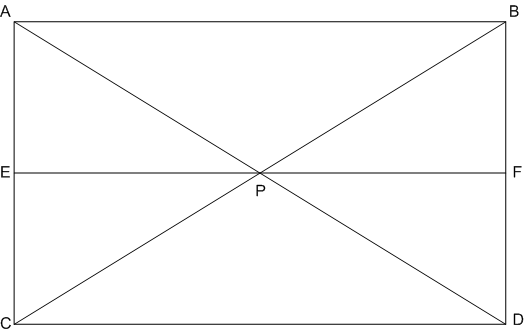
[Hint. Through P, draw a line parallel to AB.]

1556 Views

Long Answer Type

In figure, PQRS and ABRS are parallelograms and X is any point on side BR. Show that: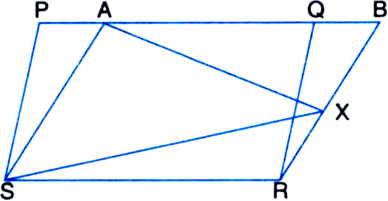

(i) ar(|| gm PQRS) = ar(|| gm ABRS)

(ii) $ar left parenthesis increment AXS right parenthesis equals 1 half ar left parenthesis space parallel to space gm space PQRS right parenthesis.$

356 Views

Short Answer Type

7. A farmer was having a field in the form of a parallelogram PQRS. She took any point A on RS and joined it to points P and Q. In how many parts the fields is divided? What are the shapes of these parts? The farmer wants to sow wheat and pulses in equal portions of the field separately. How should she do it?

256 Views

8. The diagonals of a parallelogram ABCD intersect at a point O. Through O, a line is drawn to intersect AD at P and BC at Q. Show that PQ divides the parallelogram into two parts of equal area.

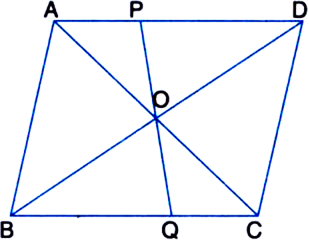
Given: The diagonals of a parallelogram ABCD intersect at a point O. Through O, a line is drawn to intersect AD at P and BC at Q.

To Prove: ar(□PDCQ) = ar(□PQBA). Proof: ∵ AC is a diagonal of || gm ABCD ∴ ar(ΔABC) = ar(ΔACD)

equals space 1 half space ar left parenthesis space parallel to space gm space ABCD right parenthesis space space space space space space space space space... left parenthesis 1 right parenthesis

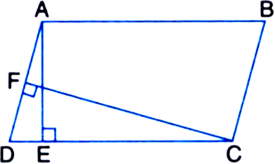
In ΔAOP and ΔCOQ,
AO = CO
| ∵ Diagonals of a parallelogram bisect each other
∠AOP = ∠COQ
| Vertically opposite angles ∠OAP = ∠OCQ
| Alternate interior angles ∴ ΔAOP = ΔCOQ
| By ASA Congruence Rule ∴ ar(ΔAOP) = ar(ΔCOQ)
| ∵ Congruent figures have equal areas ⇒ ar(ΔAOP) + ar(□OPDC)
= ar(ΔCOQ) + ar(□OPDC)
⇒ ar(ΔACD) = ar(□PDCQ)
⇒ 1/2 ar(|| gm ABCD) = ar(□PDCQ)
| From (1) ⇒ ar(□PQBA) = ar(□PDCQ)
⇒ ar(□PDCQ) = ar(□PQBA).

4000 Views

9. Prove that of all parallelograms of which the sides are given, the parallelogram which is a rectangle, has the greatest area.

2171 Views

10. In the figure, diagonals AC and BD of a trapezium ABCD with AB || CD intersect each other at O. Show that ar(Δ AOD) = ar(Δ BOC).

400 Views