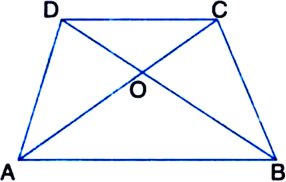
Short Answer Type
Short Answer Type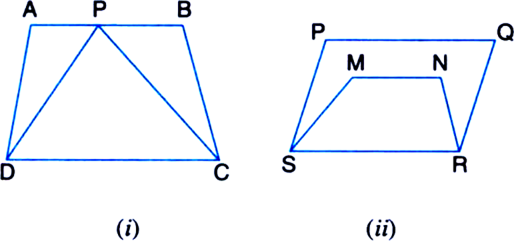
 Long Answer Type
Long Answer TypeIf E, F, G and H are respectively the mid-points of the sides of a parallelogram ABCD, show that ar(EFGH) = ![]() ar(ABCD).
ar(ABCD).
 Short Answer Type
Short Answer Type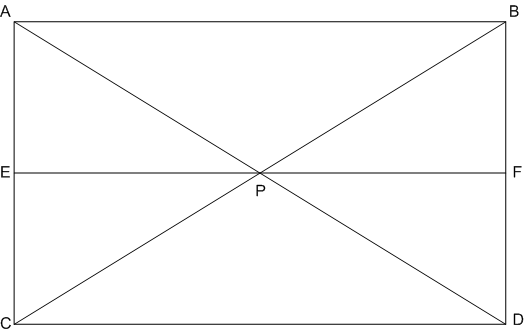
[Hint. Through P, draw a line parallel to AB.]
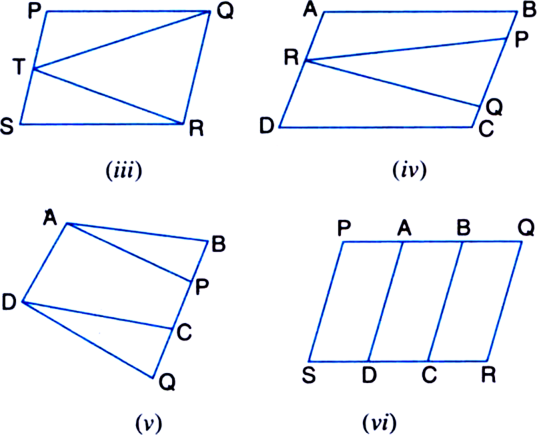
 Long Answer Type
Long Answer TypeIn figure, PQRS and ABRS are parallelograms and X is any point on side BR. Show that: 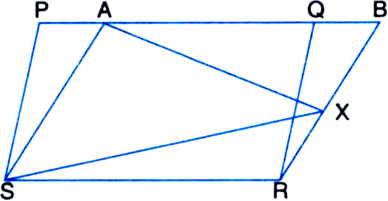
(i) ar(|| gm PQRS) = ar(|| gm ABRS)
(ii) ![]()
 Short Answer Type
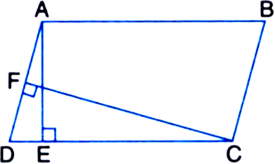
Short Answer TypeGiven: A parallelogram ABCD whose sides are given.
To Prove: The area of the parallelogram ABCD is the greatest when it is a rectangle.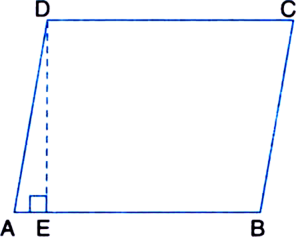
Construction: Draw DE ⊥ AB.
Proof: ar(|| gm ABCD)
= Base x Corresponding altitude = AB x DE
When parallelogram ABCD is a rectangle, then its area = AB x DA
| ∵ Then ∠DAB = 90° as such DA will be the altitude
In right triangle DEA,
∠DEA > ∠DAE
DA > DE
∵ Side opposite to greater angle of a triangle is longer ∴ ar(rectangle ABCD) > ar(|| gm ABCD)
i.e., the area of the parallelogram ABCD is the greatest when it is a rectangle.