 Short Answer Type
Short Answer Type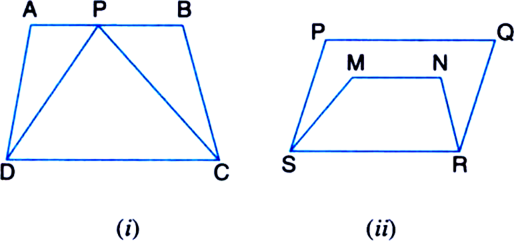
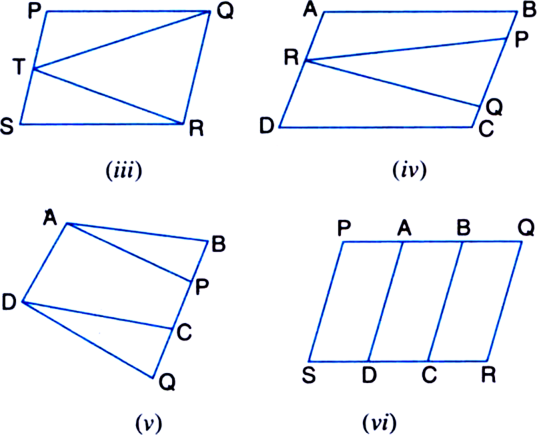
 Long Answer Type
Long Answer TypeIf E, F, G and H are respectively the mid-points of the sides of a parallelogram ABCD, show that ar(EFGH) = ![]() ar(ABCD).
ar(ABCD).
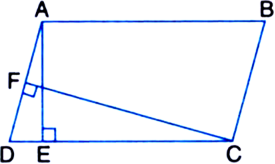
 Short Answer Type
Short Answer Type
[Hint. Through P, draw a line parallel to AB.]
 Long Answer Type
Long Answer TypeIn figure, PQRS and ABRS are parallelograms and X is any point on side BR. Show that: 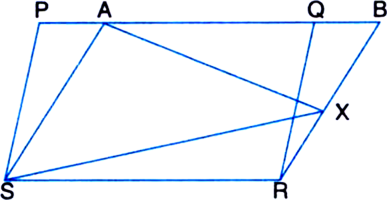
(i) ar(|| gm PQRS) = ar(|| gm ABRS)
(ii) ![]()
 Short Answer Type
Short Answer Type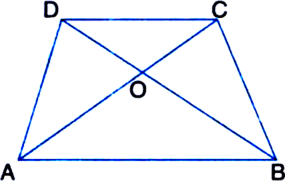
Given: Diagonals AC and BD of a trapezium ABCD with AB || CD intersect each other at O.
To Prove: ar(ΔAOD) = ar(ΔBOC)
Proof: ∵ ΔADB and ΔACB are on the same base AB and between the same parallels AB and DC ∴ ar(ΔADB) = ar(ΔACB)
∵ Two triangles on the same base and between the same parallels are equal in area ⇒ ar(ΔADB) – ar(ΔAOB)
= ar(ΔACB) – ar(ΔAOB)
| Subtracting ar(ΔAOB) from both sides Δ ar(ΔAOD) = ar(ΔBOC)
