Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Areas of Parallelograms and Triangles

Short Answer Type

11. Parallelograms on the same base and between same parallels are equal in area. Prove this.

934 Views

Long Answer Type

12. In figure, AD is median of triangle ABC, E is the mid-point of AD and F is the mid-point of AE.
Prove that $ar open parentheses ABF close parentheses equals 1 over 8 ar left parenthesis ABC right parenthesis.$

Given: AD is median of triangle ABC. E is the mid-point of AD and F is the mid-point of AE.

T o space P r o v e space colon space space ar left parenthesis ABF right parenthesis equals 1 over 8 ar left parenthesis abc right parenthesis

Proof :

because space

AD is a median of

increment ABC

therefore space space space ar left parenthesis increment ABD right parenthesis equals ar left parenthesis increment ACD right parenthesis equals 1 half ar left parenthesis increment ABC right parenthesis space space space space space space space space space space space space space space space space space space space space space space space... left parenthesis 1 right parenthesis

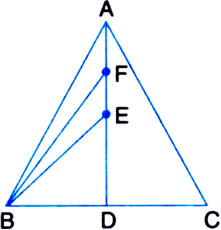
V A median of a triangle divides it into two triangles of equal areas
∵ E is the mid-point of AD
∴ BE is a median of ΔABD
∴ ar(ΔBED) = ar(ΔBEA) = 1/2 ar(ΔABD)
∵ A median of a triangle divides it into two triangles of equal areas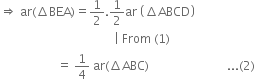

$rightwards double arrow space ar left parenthesis increment BEA right parenthesis equals 1 half.1 half ar space open parentheses increment ABCD close parentheses space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space vertical line space From space left parenthesis 1 right parenthesis space space space space space space space space space space space space space space space space space space space equals space 1 fourth space ar left parenthesis increment ABC right parenthesis space space space space space space space space space space space space space space space space space space space space space space space space space space... left parenthesis 2 right parenthesis$
∵ F is the mid-point of AE ∴ BF is a median of ΔABE

$therefore space space a r space open parentheses increment B E F close parentheses equals 1 half a r left parenthesis increment A B E right parenthesis space space space space space space$
[ $because$ A median of a triangle divides it into two triangles of equal areas]
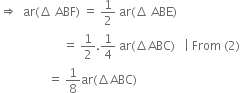
$rightwards double arrow space space ar left parenthesis increment space ABF right parenthesis space equals space 1 half space ar left parenthesis increment space ABE right parenthesis space space space space space space space space space space space space space space space space space space space space space equals space 1 half.1 fourth space ar left parenthesis increment ABC right parenthesis space space space vertical line space From space left parenthesis 2 right parenthesis space space space space space space space space space space space space space space space space equals space 1 over 8 ar left parenthesis increment ABC right parenthesis space$

380 Views

Short Answer Type

13. ABCD is a quadrilateral and BD is one of its diagonals as shown in figure. Show that ABCD is a parallelogram and find its area.

2248 Views

14. In the given figure, AB | | DC. Show that ar(BDE) = ar(ACED).

306 Views

15.

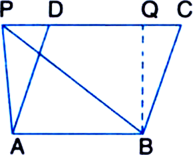
In the given figure, ABED is a parallelogram in which DE = EC. Show that area (ABF) = area (BEC)

420 Views

16. Areas of triangles on the same bases and between the same parallels are equal in. Prove it.

128 Views

17. Prove that the area of a trapezium is equal to half of the product of its height and sum of parallel sides.

721 Views

18.

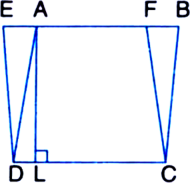
In the following figure, ABCD is a parallelogram and EFCD is a rectangle. Also, AL ⊥ DC. Prove that
(i) ar(ABCD) = ar(EFCD)
(ii) ar(ABCD) = DC x AL.

786 Views

19. If a triangle and a parallelogram are on the same base and between the same parallels, then prove that the area of the triangle is equal to half the area of the parallelogram.