Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Areas of Parallelograms and Triangles

Short Answer Type

11. Parallelograms on the same base and between same parallels are equal in area. Prove this.

934 Views

Long Answer Type

12. In figure, AD is median of triangle ABC, E is the mid-point of AD and F is the mid-point of AE.
Prove that

ar open parentheses ABF close parentheses equals 1 over 8 ar left parenthesis ABC right parenthesis.

380 Views

Short Answer Type

13. ABCD is a quadrilateral and BD is one of its diagonals as shown in figure. Show that ABCD is a parallelogram and find its area.

Given: ABCD is a quadrilateral and BD is one of its diagonals.
To Prove: ABCD is a parallelogram and to determine its area.
Proof: ∠ABD = ∠BDC (= 90°) | Given But these angles form a pair of equal alternate
interior angles for lines AB, DC and a transversal BD AB || DC
Also, AD = DC (= 3 cm) | Given
Hence, quadrilateral ABCD is a parallelogram. A quadrilateral is a parallelogram if its one pair of opposite sides are parallel and equal Now,
ar(||gm ABCD) = Base x corresponding altitude
= 3x4 = 12 cm²

2248 Views

14. In the given figure, AB | | DC. Show that ar(BDE) = ar(ACED).

306 Views

15.

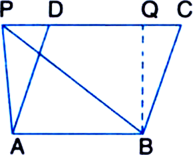
In the given figure, ABED is a parallelogram in which DE = EC. Show that area (ABF) = area (BEC)

420 Views

16. Areas of triangles on the same bases and between the same parallels are equal in. Prove it.

128 Views

17. Prove that the area of a trapezium is equal to half of the product of its height and sum of parallel sides.

721 Views

18.

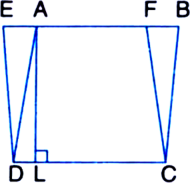
In the following figure, ABCD is a parallelogram and EFCD is a rectangle. Also, AL ⊥ DC. Prove that
(i) ar(ABCD) = ar(EFCD)
(ii) ar(ABCD) = DC x AL.

786 Views

19. If a triangle and a parallelogram are on the same base and between the same parallels, then prove that the area of the triangle is equal to half the area of the parallelogram.

102 Views

20. In the figure, PQRS is a parallelogram with PQ = 12 cm, altitudes corresponding to PQ and SP are respectively 8 cm and 10 cm. Find SP.

202 Views