 Short Answer Type
Short Answer Type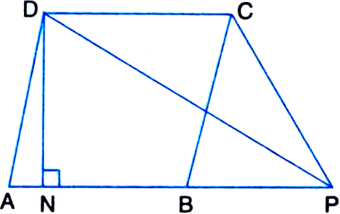
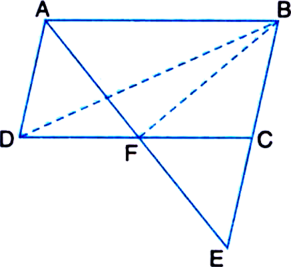

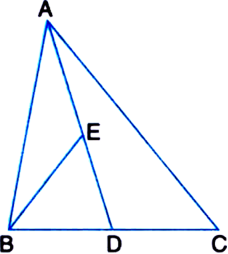
(1)
∵ A median of a triangle divides it into two triangles of equal areas.
In ΔABD,
∵ BE is a median.
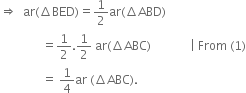
 Long Answer Type
Long Answer TypeD, E and F are respectively the midpoints of the sides BC, CA and AB of a ΔABC. Show that:
(i) BDEF is a parallelogram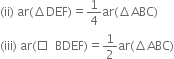
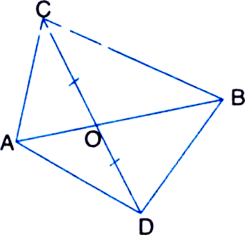
In figure, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that:
(i) ar(ΔDOC) = ar(ΔAOB)
(ii) ar(ΔDCB) = ar(ΔACB)
(iii) DA || CB or ABCD is a parallelogram.
[Hint. From D and B, draw perpendiculars to AC.]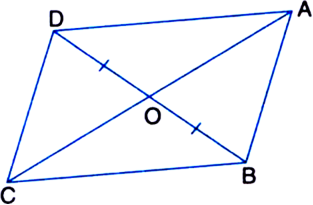
 Short Answer Type
Short Answer Type