 Short Answer Type
Short Answer Type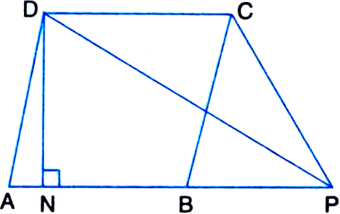

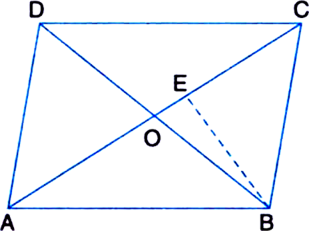

But OA = OC
∴ ar(ΔOAB) = ar(ΔOBC) ...(1)
Similarly,
ar(ΔOBC) = ar(ΔOCD) ...(2)
and, ar(ΔOCD) = ar(ΔODA) ...(3)
From (1), (2) and (3), ar(ΔOAB) = ar(ΔOBC)
= ar(ΔOCD) = ar(ΔODA).
 Long Answer Type
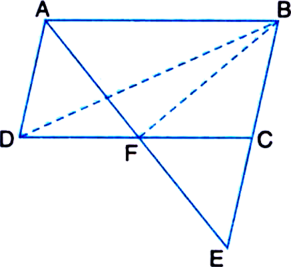
Long Answer TypeD, E and F are respectively the midpoints of the sides BC, CA and AB of a ΔABC. Show that:
(i) BDEF is a parallelogram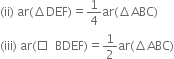
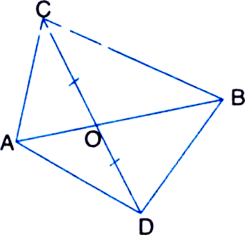
In figure, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that:
(i) ar(ΔDOC) = ar(ΔAOB)
(ii) ar(ΔDCB) = ar(ΔACB)
(iii) DA || CB or ABCD is a parallelogram.
[Hint. From D and B, draw perpendiculars to AC.]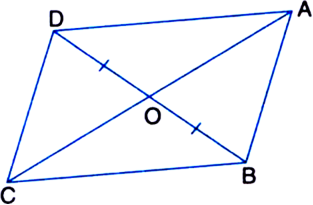
 Short Answer Type
Short Answer Type