 Short Answer Type
Short Answer Type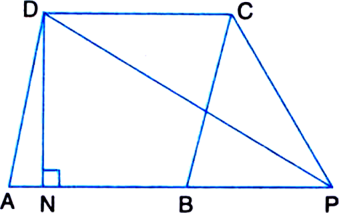
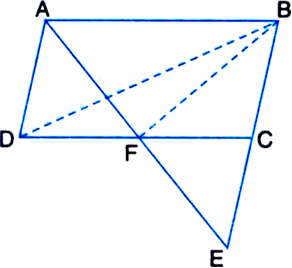

Given: ABC and ABD are two triangles on the same base AB. Line segment CD is bisected by AB at O.
To Prove: ar(ΔABC) = ar(ΔABD).
Proof: ∵ Line segment CD is bisected by AB
at O.
∴ OC = OD BO is a median of ΔBCD and AO is a median of ΔACD
∵ BO is a median of ΔBCD
∴ ar(ΔOBC) = ar(ΔOBD) ...(1)
∵ A median of a triangle divides it into two triangles of equal areas
∵ AO is a median of ΔACD
∴ ar(ΔOAC) = ar(ΔOAD) ...(2)
∵ A median of a triangle divides it into two triangles of equal areas
Adding (1) and (2), we get ar(ΔOBC) + ar(ΔOAC)
= ar(ΔOBD) + ar(ΔOAD)
⇒ ar(ΔABC) = ar(ΔABD).
 Long Answer Type
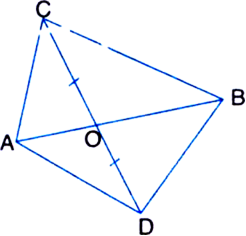
Long Answer TypeD, E and F are respectively the midpoints of the sides BC, CA and AB of a ΔABC. Show that:
(i) BDEF is a parallelogram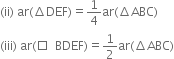
In figure, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that:
(i) ar(ΔDOC) = ar(ΔAOB)
(ii) ar(ΔDCB) = ar(ΔACB)
(iii) DA || CB or ABCD is a parallelogram.
[Hint. From D and B, draw perpendiculars to AC.]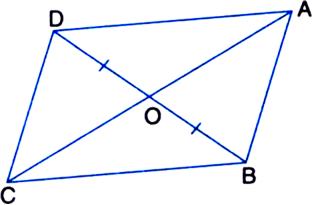
 Short Answer Type
Short Answer Type