 Short Answer Type
Short Answer Type

 Long Answer Type
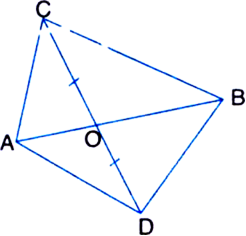
Long Answer TypeD, E and F are respectively the midpoints of the sides BC, CA and AB of a ΔABC. Show that:
(i) BDEF is a parallelogram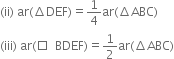
Given: D, E and F are respectively the midpoints of the sides BC, CA and AB of a ΔABC.
To Prove: (i) □BDEF is a parallelogram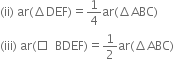
Proof: (i) In ΔABC,
∵ F is the mid-point of side AB and
E is the mid-point of side AC.
∴ EF || BC
∵ In a triangle, the line segment joining the mid-points of any two sides is parallel to the third side.
⇒ EF || BD ...(1)
Similarly, ED || BF ...(2)
In view of (1) and (2),
□ BDEF is a parallelogram.
∵ A quadrilateral is a parallelogram
if its opposite sides are parallel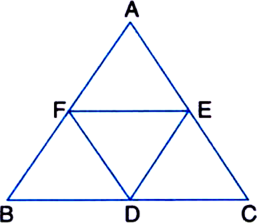
(ii) As in (i), we can prove that
□AFDE and □FDCE are parallelograms.
∵ FD is a diagonal of || gm BDEF.
ar(ΔFBD) = ar(ΔDEF) ...(3) Similarly, ar(ΔDEF) = ar(ΔFAE) ...(4) and, ar(ΔDEF) = ar(ΔDCE) ...(5)
From (3), (4) and (5), we have ar(ΔFBD) = ar(ΔDEF)
= ar(ΔFAE) = ar(ΔDCE) ...(6)
∵ ΔABC is divided into four non-overlapping triangles ΔFBD, ΔDEF, ΔFAE and ΔDCE.
∴ ar(ΔABC) = ar(ΔFBD) + ar(ΔDEF) + ar(ΔFAE) + ar(ΔDCE) = 4 ar(ΔDEF) | From (6)
⇒ ar(ΔDEF) = 1/2 ar(ΔABC). ...(7)
4
(iii) ar(□BDEF)
= ar(ΔFBD) + ar(ΔDEF)
= ar(ΔDEF) + ar(ΔDEF)
| From (3)
= 2 ar(ΔDEF)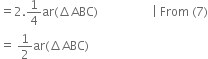
In figure, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that:
(i) ar(ΔDOC) = ar(ΔAOB)
(ii) ar(ΔDCB) = ar(ΔACB)
(iii) DA || CB or ABCD is a parallelogram.
[Hint. From D and B, draw perpendiculars to AC.]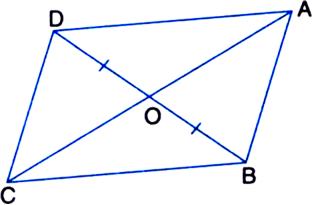
 Short Answer Type
Short Answer Type