 Short Answer Type
Short Answer Type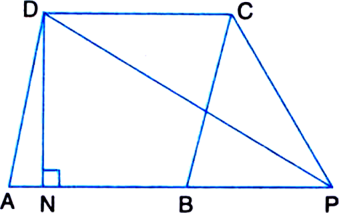
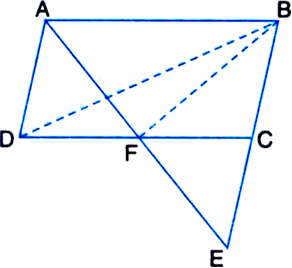

 Long Answer Type
Long Answer TypeD, E and F are respectively the midpoints of the sides BC, CA and AB of a ΔABC. Show that:
(i) BDEF is a parallelogram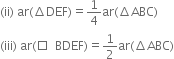
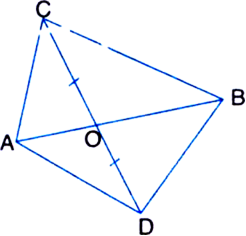
In figure, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that:
(i) ar(ΔDOC) = ar(ΔAOB)
(ii) ar(ΔDCB) = ar(ΔACB)
(iii) DA || CB or ABCD is a parallelogram.
[Hint. From D and B, draw perpendiculars to AC.]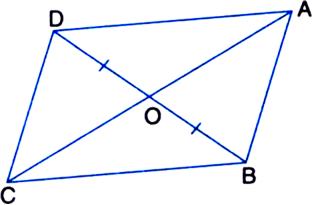
 Short Answer Type
Short Answer TypeGiven: D and E are points on sides AB and AC respectively of ΔABC such that ar(ΔDBC) = ar(ΔEBC).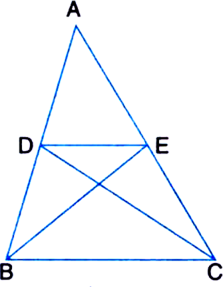
To Prove: DE || BC.
Proof: ∵ ΔDBC and ΔEBC are on the same base BC and have equal areas.
Their altitudes must be the same.
∴ DE || BC.
